analytic geometry is a field of math where is it possible represent geometric elements, like points, lines, triangles, quadrilaterals and circles, using algebraic expressions. Algebraic expressions are derived from the idea of joining points that follow a certain pattern. These points are arranged in a coordinate system proposed by Rene Descartes.
Know more: Triangle area through analytic geometry
What does analytic geometry study?
Analytical geometry has as its main objective describe geometric objects using a coordinate system, O Cartesian plane. This consists of two real axes perpendicular to each other. The horizontal axis is called the abscissa axis, and the vertical axis is called the ordinate axis.

Important Concepts of Analytical Geometry
distance between two points
The distance between points A (xTheyThe) and B (xByB) is defined by the line segment AB, which we'll denote dAB. See how to get the size of this segment, ie the distance.
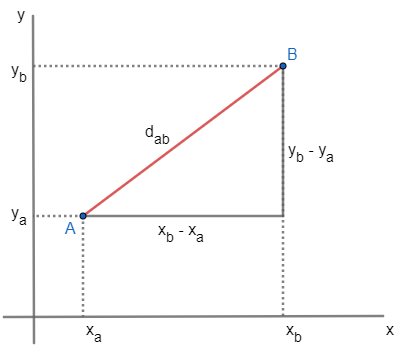
Note that the distance between points A and B is the hypotenuse of the triangle, so to determine it, let's use the Pythagorean theorem.
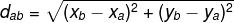
Example
Calculate the distance between points A (0, 0) and B (4, 2).
Substituting the coordinate values in the formula, we have:

To go deeper into this concept of analytic geometry, read our text: Distance between two points.
Do not stop now... There's more after the advertising ;)
point coordinates average
At plane geometry, the midpoint is the point that divides the line segment AB in half, that is, into two equal parts. In analytic geometry, the midpoint coordinates are given by:
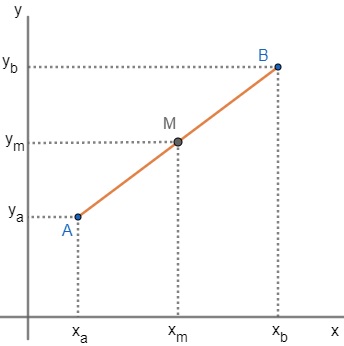
The coordinate of the midpoint, that is, from point M, is given by:
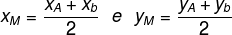
Example
Determine the midpoint of segment AB, knowing that A (2, 1) and B (6, 5).
Substituting the coordinate values in the formula, we have:
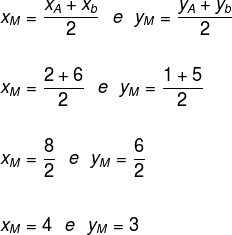
Three Alignment Condition points
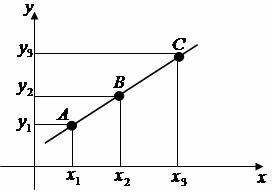
Consider three points — A(xTheyThe), B(xByB) and C (xçyç) — distinct in plane. We will say that the points are collinear if the determinant below is equal to zero. We can also say that they are collinear if there is a line that contains them.

Read too:Matrix equations: how to solve?
solved exercises
Question 1 – (PUC-SP) Points A (3, 5), B (1, -1) and C (x, -16) belong to the same line. Determine the value of x.
Solution
In the statement it was given that the points belong to the same line, that is, points A, B and C are collinear. Therefore, the determinant is equal to zero.
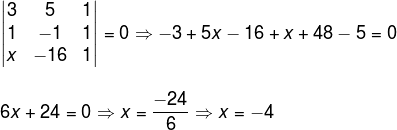
by Robson Luiz
Maths teacher
Would you like to reference this text in a school or academic work? Look:
LUIZ, Robson. "Analytical geometry"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/definicao-geometria-analitica.htm. Accessed on June 28, 2021.