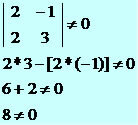Distance between two points in space

THE distance between two points is one of the most important concepts of Analytical Geometry. It is through this concept that most of the definitions and properties of geometric figures are constructed.

THE distance between two points it is the smallest straight segment that connects them. Thus, the job of finding a distance boils down to measuring the length of a straight line segment.

Usually, in Analytical Geometry, the measures of straight segments are made through the Pythagorean theorem. In this way, this same theorem is used to arrive at a formula for calculating the distance between two points.

Formula demonstration

Note, in the figure below, the points A = (x_THEy_THE, z_THE) and B = (x_By_B, z_B). The first step is to build the smallest segment of straight line that connects them. To do this, just connect them with a straight line.

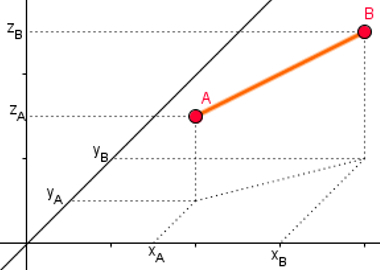
Once this is done, observe in the figure below the same segment seen from above:

Note that the top view reduces the first part of the problem to distance between two points on the plane

. We will use the Pythagorean Theorem to find the square of the length of segment A'B', projection of AB onto the xy plane. Remember, however, that the collars to be considered have sizes x_B – x_THE and y_B - y_THE.

Do not stop now... There's more after the advertising ;)

Once this is done, we will use the Pythagorean theorem again to calculate the length of AB. Note that AB is the hypotenuse of a right triangle where A'B' is leg and base (this segment is parallel to segment projection AB and has the same size) and z_B – z_THE is the other leg and height.

Thus, by the theorem of Pythagoras, we have:

This ends the demonstration, once the length of segment AB has been found.

Formula of the distance between two points in space

From the above calculations, the distance between two points in space, denoted by d_AB, is defined as follows:

To use this formula, simply substitute the numerical values ​​of the coordinates of points A and B and perform the calculations. Look at the example:

Calculate the distance between points A = (0,2.2) and B = (-2, 0, 1):

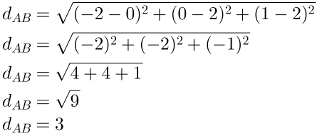
By Luiz Paulo Moreira
Graduated in Mathematics

Would you like to reference this text in a school or academic work? Look:

SILVA, Luiz Paulo Moreira. "Distance between two points in space"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/distancia-entre-dois-pontos-no-espaco.htm. Accessed on June 28, 2021.