Sine, Cosine and Tangent are the names given to trigonometric ratios. Most of the problems involving distance calculations are solved using the trigonometry. And for that, it is very important to understand its fundamentals, starting with the right triangle.
Trigonometric ratios are also very important, as they relate the measurements on both sides of the triangle with one of the acute angles, associating this relationship with a real number.

See more: Identifying the quadrants of the trigonometric cycle
Right Triangle Features
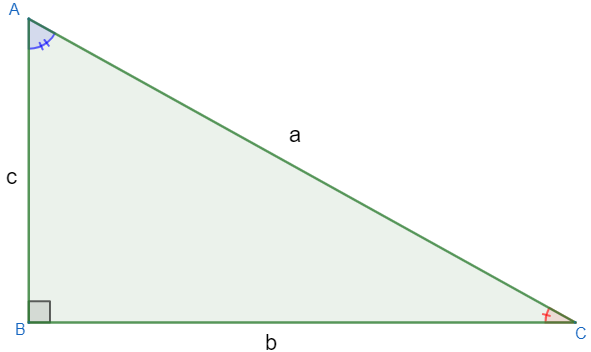
The right triangle is formed by a angle 90° (straight angle). The other angles are smaller than 90º, that is, they are acute, and, in addition, we know that the biggest sides are always opposite the biggest angles. In the right triangle, the largest side is called the hypotenuse and is "in front" of the right angle, the other sides are called peccaries.
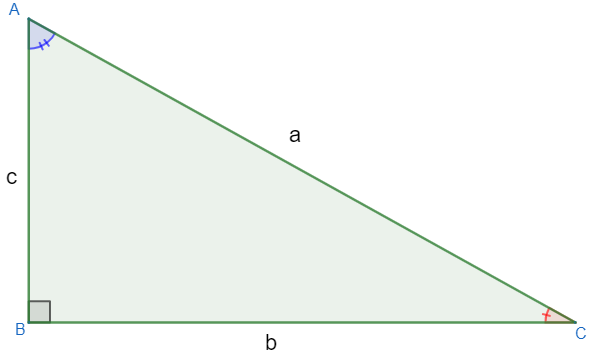
In the triangle above, we have that the sides that measure c and b are the legs, and the side that measures a is the hypotenuse. In every right triangle, the relationship knew as
Pythagorean theorem is valid.The2 = b2 + c2
The collared peccaries, from now on, will also be given special names. The nomenclatures of the legs will depend on the reference angle. Considering the angle in blue in the image above, we have that the side that measures b is the opposite leg, and the side that is next to the angle, that is, that measures c is the adjacent leg.
Do not stop now... There's more after the advertising ;)
Sine
Before defining a formula for the sine of an angle, let's understand the idea of sine. Imagine a ramp, on which we can determine the reason between height and course, right? This ratio will be called the sine of the angle α.
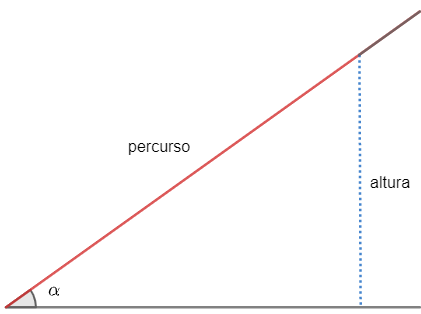
Thus,
sin α = height
route
cosine
Analogous to the idea of sine, we have the sense of cosine, however, in a ramp, the cosine is the ratio between the distance from the ground and the path along the ramp.
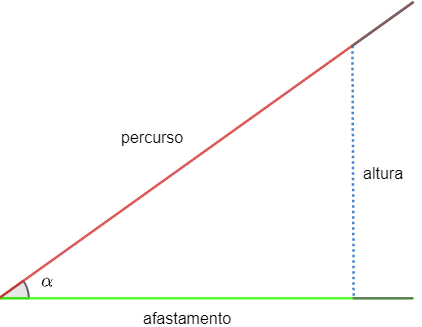
Thus:
cos α = removal
route
Tangent
Also similar to the ideas of sine and cosine, the tangent is the ratio between the height and the distance of a ramp.

Thus:
tg α = height
removal
The tangent gives us the climb rate.
Read too: Trigonometry in any triangle
Relationship between sine, cosine and tangent
Generally speaking, we can then define sine, cosine and tangent in any right triangle using the previous ideas. See below:
First taking the angle α as a reference, we have:
sin α = opposite side = ç
hypotenuse to
cos α = adjacent catet = B
hypotenuse to
tg α = opposite side = ç
Adjacent catet b
Now taking the angle β as a reference, we have:
sin β = opposite side = B
hypotenuse to
cos β = adjacent catet = ç
hypotenuse to
tg β = opposite side = B
adjacent cathetus c
Trigonometric Tables
There are three angle values we must know. Are they:

The other values are given in the exercises' statements or can be checked in the following table, but don't worry, it is not necessary to have them memorized (except for the ones in the previous table).
Angle (°) |
sine |
cosine |
tangent |
Angle (°) |
sine |
cosine |
tangent |
1 |
0,017452 |
0,999848 |
0,017455 |
46 |
0,71934 |
0,694658 |
1,03553 |
2 |
0,034899 |
0,999391 |
0,034921 |
47 |
0,731354 |
0,681998 |
1,072369 |
3 |
0,052336 |
0,99863 |
0,052408 |
48 |
0,743145 |
0,669131 |
1,110613 |
4 |
0,069756 |
0,997564 |
0,069927 |
49 |
0,75471 |
0,656059 |
1,150368 |
5 |
0,087156 |
0,996195 |
0,087489 |
50 |
0,766044 |
0,642788 |
1,191754 |
6 |
0,104528 |
0,994522 |
0,105104 |
51 |
0,777146 |
0,62932 |
1,234897 |
7 |
0,121869 |
0,992546 |
0,122785 |
52 |
0,788011 |
0,615661 |
1,279942 |
8 |
0,139173 |
0,990268 |
0,140541 |
53 |
0,798636 |
0,601815 |
1,327045 |
9 |
0,156434 |
0,987688 |
0,158384 |
54 |
0,809017 |
0,587785 |
1,376382 |
10 |
0,173648 |
0,984808 |
0,176327 |
55 |
0,819152 |
0,573576 |
1,428148 |
11 |
0,190809 |
0,981627 |
0,19438 |
56 |
0,829038 |
0,559193 |
1,482561 |
12 |
0,207912 |
0,978148 |
0,212557 |
57 |
0,838671 |
0,544639 |
1,539865 |
13 |
0,224951 |
0,97437 |
0,230868 |
58 |
0,848048 |
0,529919 |
1,600335 |
14 |
0,241922 |
0,970296 |
0,249328 |
59 |
0,857167 |
0,515038 |
1,664279 |
15 |
0,258819 |
0,965926 |
0,267949 |
60 |
0,866025 |
0,5 |
1,732051 |
16 |
0,275637 |
0,961262 |
0,286745 |
61 |
0,87462 |
0,48481 |
1,804048 |
17 |
0,292372 |
0,956305 |
0,305731 |
62 |
0,882948 |
0,469472 |
1,880726 |
18 |
0,309017 |
0,951057 |
0,32492 |
63 |
0,891007 |
0,45399 |
1,962611 |
19 |
0,325568 |
0,945519 |
0,344328 |
64 |
0,898794 |
0,438371 |
2,050304 |
20 |
0,34202 |
0,939693 |
0,36397 |
65 |
0,906308 |
0,422618 |
2,144507 |
21 |
0,358368 |
0,93358 |
0,383864 |
66 |
0,913545 |
0,406737 |
2,246037 |
22 |
0,374607 |
0,927184 |
0,404026 |
67 |
0,920505 |
0,390731 |
2,355852 |
23 |
0,390731 |
0,920505 |
0,424475 |
68 |
0,927184 |
0,374607 |
2,475087 |
24 |
0,406737 |
0,913545 |
0,445229 |
69 |
0,93358 |
0,358368 |
2,605089 |
25 |
0,422618 |
0,906308 |
0,466308 |
70 |
0,939693 |
0,34202 |
2,747477 |
26 |
0,438371 |
0,898794 |
0,487733 |
71 |
0,945519 |
0,325568 |
2,904211 |
27 |
0,45399 |
0,891007 |
0,509525 |
72 |
0,951057 |
0,309017 |
3,077684 |
28 |
0,469472 |
0,882948 |
0,531709 |
73 |
0,956305 |
0,292372 |
3,270853 |
29 |
0,48481 |
0,87462 |
0,554309 |
74 |
0,961262 |
0,275637 |
3,487414 |
30 |
0,5 |
0,866025 |
0,57735 |
75 |
0,965926 |
0,258819 |
3,732051 |
31 |
0,515038 |
0,857167 |
0,600861 |
76 |
0,970296 |
0,241922 |
4,010781 |
32 |
0,529919 |
0,848048 |
0,624869 |
77 |
0,97437 |
0,224951 |
4,331476 |
33 |
0,544639 |
0,838671 |
0,649408 |
78 |
0,978148 |
0,207912 |
4,70463 |
34 |
0,559193 |
0,829038 |
0,674509 |
79 |
0,981627 |
0,190809 |
5,144554 |
35 |
0,573576 |
0,819152 |
0,700208 |
80 |
0,984808 |
0,173648 |
5,671282 |
36 |
0,587785 |
0,809017 |
0,726543 |
81 |
0,987688 |
0,156434 |
6,313752 |
37 |
0,601815 |
0,798636 |
0,753554 |
82 |
0,990268 |
0,139173 |
7,11537 |
38 |
0,615661 |
0,788011 |
0,781286 |
83 |
0,992546 |
0,121869 |
8,144346 |
39 |
0,62932 |
0,777146 |
0,809784 |
84 |
0,994522 |
0,104528 |
9,514364 |
40 |
0,642788 |
0,766044 |
0,8391 |
85 |
0,996195 |
0,087156 |
11,43005 |
41 |
0,656059 |
0,75471 |
0,869287 |
86 |
0,997564 |
0,069756 |
14,30067 |
42 |
0,669131 |
0,743145 |
0,900404 |
87 |
0,99863 |
0,052336 |
19,08114 |
43 |
0,681998 |
0,731354 |
0,932515 |
88 |
0,999391 |
0,034899 |
28,63625 |
44 |
0,694658 |
0,71934 |
0,965689 |
89 |
0,999848 |
0,017452 |
57,28996 |
45 |
0,707107 |
0,707107 |
1 |
90 |
1 |
Also know: Secant, cosecant and cotangent
solved exercises
question 1 - Determine the value of x and y in the following triangle.

Solution:
See in the triangle that the angle given was 30°. Still looking at the triangle, we have the side that measures x it's the opposite leg at the angle of 30°, and the side that measures y it's the adjacent leg at an angle of 30°. Thus, we must look for a trigonometric ratio that relates what we are looking for with what is given (hypotenuse). Soon:
sin 30° = opposite side
Hypotenuse
cos 30° = adjacent catet
Hypotenuse
Determined the value of x:
sin 30° = opposite side
Hypotenuse
sin 30° = x
2
Looking at the table, we have to:
sin 30° = 1
2
Substituting it in the equation, we will have:
1 = x
2 2
x = 1
Similarly, we will consider
Thus:
Cos 30° = √3
2
cos 30° = adjacent catet
Hypotenuse
cos 30° = Y
2
√3 = Y
2 2
y = √3
question 2 – (PUC-SP) What is the value of x in the following figure?

Solution:
Viewing the larger triangle, notice that y is opposite the 30° angle and that 40 is the hypotenuse, that is, we can use the trigonometric sine ratio.
sin 30° = Y
40
1 = Y
2 40
2 y = 40
y = 20
Now looking at the smaller triangle, see that we have the value of the opposite side and we look for the value of x, which is the adjacent side. The trigonometric relationship involving these two legs is the tangent. Thus:
tg 60° = 20
x
√3= 20
x
√3 x = 20
x = 20 · √3
√3 √3
x = 20√3
3
by Robson Luiz
Maths teacher
Would you like to reference this text in a school or academic work? Look:
LUIZ, Robson. "Sine, Cosine and Tangent"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/seno-cosseno-tangente-angulos.htm. Accessed on June 27, 2021.