Proportional quantities have their values increased or decreased in a relationship that can be classified as direct or inverse proportionality.
What are proportional quantities?
A quantity is defined as something that can be measured or calculated, whether it is velocity, area or volume of a material, and is useful to compare with other measurements, often of the same unit, representing a reason.
Proportion is a relationship of equality between ratios and, thus, presents the comparison of two quantities in different situations.
The equality between a, b, c and d is read as follows: a is to b as c is to d.
The relationship between the quantities can occur in a directly or inversely proportional way.
How do directly and inversely proportional quantities work?
When the variation of one quantity causes the other to vary in the same proportion, we have a direct proportionality. Inverse proportionality is observed when a change in one quantity produces an opposite change in the other.
direct proportionality
Two quantities are directly proportional when the variation of one implies the variation of the other in the same proportion, that is, by doubling one of them, the other also doubles; reducing by half, the other also reduces by the same amount... and so on.
Graphically, the directly proportional variation of a quantity in relation to another form a straight line that passes through the origin, since we have y = k.x, where k is a constant.
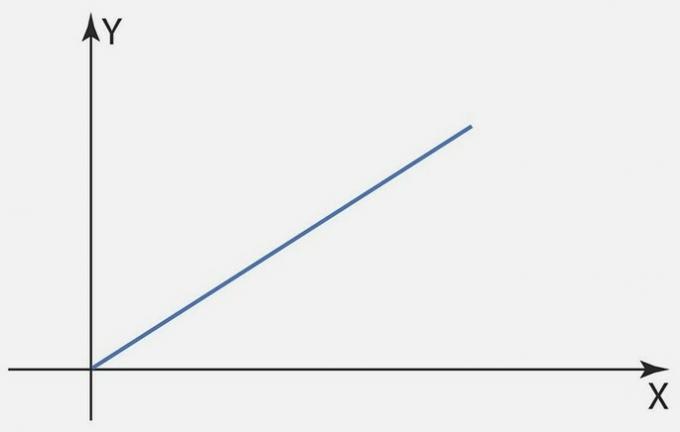
Example of direct proportionality
A printer, for example, has the ability to print 10 pages per minute. If we double the time, we double the number of pages printed. Likewise, if we stop the printer in half a minute, we get half the number of expected prints.
Now, we will see with numbers the relationship between the two quantities.
In a print shop, prints of textbooks are made. In 2 hours, 40 prints are made. In 3 hours, the same machine produces another 60 impressions, in 4 hours, 80 impressions, and in 5 hours, 100 impressions.
| Time (hours) | 2 | 3 | 4 | 5 |
| Impressions (number) | 40 | 60 | 80 | 100 |
The constant of proportionality between the quantities is found by the ratio between the working time of the machine and the number of copies made.
The quotient of this sequence (1/20) is called proportionality constant (k).
The working time (2, 3, 4 and 5) is directly proportional to the number of copies (40, 60, 80 and 100), because by doubling the working time the number of copies also doubles.
inverse proportionality
Two quantities are inversely proportional when the increase of one implies the reduction of the other, that is, by doubling a quantity, the corresponding one reduces by half; tripling one magnitude, the other reduces it to a third... and so on.
Graphically, the inversely proportional variation of one quantity in relation to another forms a hyperbola, since we have y = k/x, where k is a constant.

Inverse Proportion Example
When speed is increased, the time to complete a course is shorter. Likewise, by decreasing the speed, more time will be needed to make the same path.
See below an application of the relationship between these quantities.
João decided to count the time it took to cycle from home to school at different speeds. Note the recorded sequence.
| Time (min) | 2 | 4 | 5 | 1 |
| Speed (m/s) | 30 | 15 | 12 | 60 |
We can make the following relationship with the sequence numbers:
Writing as equal reasons, we have:
In this example, the time sequence (2, 4, 5 and 1) is inversely proportional to the average pedaling speed (30, 15, 12 and 60) and the proportionality constant (k) between these quantities is 60.
Note that when a sequence number doubles, the corresponding sequence number is halved.
See too: Proportionality
Exercises commented on directly and inversely proportional quantities
question 1
Classify the quantities listed below into directly or inversely proportional.
a) Fuel consumption and kilometers traveled by a vehicle.
b) Number of bricks and area of a wall.
c) Discount given on a product and the final price paid.
d) Number of taps with the same flow and time to fill a pool.
Correct answers:
a) Directly proportional quantities. The more kilometers a vehicle travels, the greater the fuel consumption to complete the route.
b) Directly proportional quantities. The larger the area of a wall, the greater the number of bricks that will be part of it.
c) Inversely proportional quantities. The greater the discount given on the purchase of a product, the lower the amount that will be paid for the merchandise.
d) Inversely proportional quantities. If the faucets have the same flow, they release the same amount of water. Therefore, the more taps open, the less time it takes for the amount of water needed to fill the pool to be released.
question 2
Pedro has a swimming pool in his house that measures 6 m in length and holds 30,000 liters of water. His brother Antônio also decides to build a swimming pool with the same width and depth, but 8 m long. How many liters of water fit in Antônio's pool?
a) 10 000 L
b) 20 000 L
c) 30,000 L
d) 40 000 L
Correct answer: d) 40 000 L.
Grouping the two quantities given in the example, we have:
| magnitudes | Peter | Antonio |
| Pool length (m) | 6 | 8 |
| Water flow (L) | 30 000 | x |
According to the fundamental property of proportions, in the relation between the quantities, the product of the extremes is equal to the product of the means and vice versa.
To resolve this issue we use the x as unknown, that is, the fourth value that must be calculated from the three values given in the statement.
Using the fundamental property of proportions, we calculate the product of the means and the product of the extremes to find the value of x.
Note that among the quantities there are direct proportionality: the greater the length of the pool, the greater the amount of water it holds.
See too: Ratio and Proportion
question 3
In a cafeteria, Mr. Alcides prepares strawberry juice every day. In 10 minutes and using 4 blenders, the cafeteria can prepare the juices that customers order. To cut down on the preparation time, Alcides doubled the number of blenders. How long did it take for the juices to be ready with the 8 blenders working?
a) 2 min
b) 3 min
c) 4 min
d) 5 min
Correct answer: d) 5 min.
|
Blenders (number) |
Time (minutes) |
| 4 | 10 |
| 8 | x |
Note that among the magnitudes of the question there are inverse proportionality: the more blenders that are making juice, the less time it will take for everyone to be ready.
Therefore, to solve this problem the time magnitude must be inverted.
We then apply the fundamental property of proportion and resolve the issue.
Don't stop there, you may also be interested in:
- Exercises on reason and proportion
- Simple and compound rule of three
- Exercises on rule of three



