Points, straight, plans and space are primitive notions for Mathematics. Thus, we have a good idea of what these objects are and their shapes, but it is not possible to define them. In this text, we will study the plan.
What is plan?
O flat is a set of lines arranged side by side so that there are no spaces between these lines and that it is also infinite, and does not describe any curves.

Graphical view of a part of the straight line on the left and part of a plane on the right
plans in postulates
Postulate (or axiom) is a fact that needs no proof to be accepted as truth. The only guarantee that points, straight lines and plans exist are the postulates of existence. In the specific case of the plan, this postulate is:
“There is a plan. There are points in it and outside it."
To build a flat, there is a postulate of determination:
“Three non-collinear points determine a single plane that contains them.”
How to get plans?
You plans can be obtained in a few different ways.
Through the postulate of determination
To do so, it is enough to note that three non-collinear points determine a flat single. Therefore, obtaining three non-collinear points is one of the ways to obtain a plan.

Plan determined by three distinct non-collinear points
Through a straight line and a point outside of it
Three non-collinear points determine a flat. So take two distinct points on the line and the point outside of it and you will have the three points you need to determine the flat.
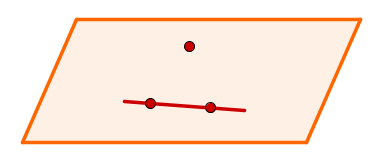
Plan determined by a straight line and a point outside it
through two competing straight lines
Since two competing lines meet at point A, take two other points, one on each line. These last two points and point A are not collinear and this determines the flat.
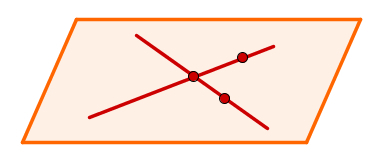
Plan determined by two competing straight lines
through two parallel lines non-coincident
Take two distinct points on one of the lines and a point on the other. This will highlight three non-collinear points that are sufficient to determine a flat.
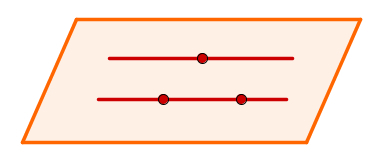
Plane determined by two non-coincident parallel lines
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-plano.htm
