On a polygon, the greater the number of sides, the greater the measurement of anglesinternal.
Considering the diagonals traced by only one of the vertices of a polygon, you can see that they form triangles. As we increase the sides of a polygon, the number of triangles also increases. Look:
On a quadrilateral, we managed to form two triangles.

Considering that, in each triangle, the sum of the inner angles equal is 180°, the sum of the internal angles of any quadrilateral is 2·180° = 360°.
On a polygon from five sides (pentagon), we form three triangles.
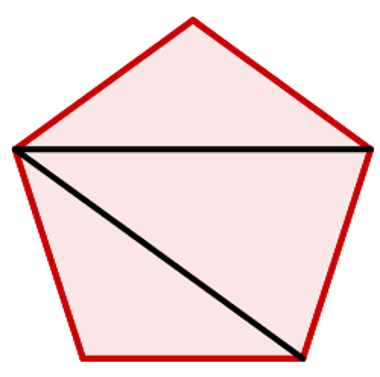
Thus, we have the sum of the inner angles of a pentagon is 180º·3 = 540º
In a six-sided polygon (hexagon), we form four triangles.
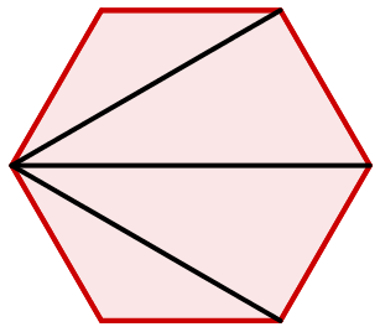
Therefore, the sum of the interior angles is 4·180° = 720°.
Sum of the internal angles of a convex polygon
We realize that the difference between the number of triangles formed and the number of sides of the polygons is always 2, so we conclude that:
Do not stop now... There's more after the advertising ;)
n = 3
si = (3 – 2)·180º = 1·180° = 180°
n = 4
si = (4 – 2)·180° = 2·180° = 360°
n = 5
si = (5 – 2)·180° = 3·180° = 540°
n = 6
si = (6 – 2)·180° = 4·180° = 720°
n = n
si = (n – 2)·180°
Therefore, the sum From inner angles of any polygon is calculated by the expression:
si = (n – 2)·180°
If you want to calculate the value of each angleinternal, just divide the sum of the anglesinternal by the number of sides of the polygon. Remember that this formula should only be used in polygonsregular, as they have the same internal angles.
Thei = si
no
Sum of the outside angles of a regular polygon
the sum of anglesexternal of any polygonconvex is equal to 360°.
Note: The sum of an internal angle with its respective external angle is equal to 180º, that is, they are supplementary.
by Mark Noah
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Sum of the internal and external angles of a convex polygon"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/soma-dos-angulos-internos-externos-um-poligono-convexo.htm. Accessed on June 27, 2021.