Bisector is a straight line perpendicular to a line segment and passing through the midpoint of this segment.
All points belonging to the bisector are equidistant from the ends of this segment.
Remembering that, unlike the line, which is infinite, the line segment is limited by two points on a line. That is, it is considered a part of the line.

How to build the bisector?
We can build the bisector of a straight line using ruler and compass. To do this, follow these steps:
- Draw a line segment and at its ends mark point A and point B.
- Take a measure and make an opening that is a little larger than half the length of the segment.
- With this opening, place the dry end of the compass at point A and draw a semicircle. Staying with the same opening in the bar, do the same thing at point B.
- The traced semicircles intersected at two points, one above the line segment and one below. With the ruler, join these two points, this line drawn is the bisector of segment AB.

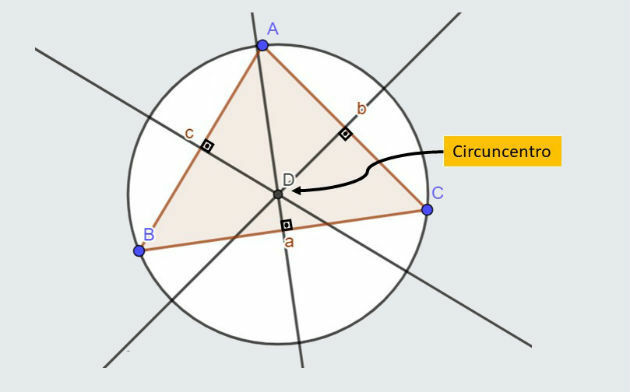
Bisector of a triangle
The bisectors of a triangle are perpendicular lines drawn through the midpoint of each of its sides. Thus, a triangle has 3 bisectors.
The meeting point of these three bisectors is called circumcenter. This point, which is the same distance from each of its vertices, is the center of the circumscribed circle in the triangle.
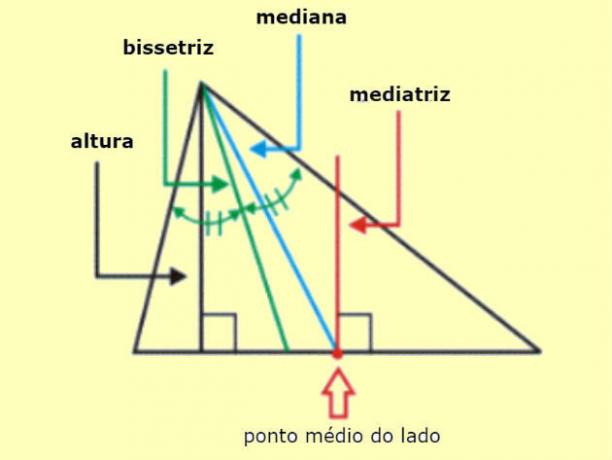
Median, bisector and height of a triangle
In a triangle, in addition to bisectors, we can construct medians, which are segments of straight lines that also pass through the midpoint of the sides.
The difference is that while the bisector forms a angle 90º with the side, the median joins the vertex to the midpoint of the opposite sides, forming an angle that may or may not be 90º.
We can still plot heights and bisectors. The height is also perpendicular to the sides of the triangle, but part of its vertex. Unlike the bisector, the height does not necessarily pass through the midpoint of the side.
Starting from the vertex, we can trace the internal bisectors, which are segments of straight lines that divide the angles of the triangle into two other angles of the same measure.
In a triangle, we can draw three medians and they meet at a point called barycenter. This point is called the center of gravity of a triangle.
The barycenter divides the medians into two parts, as the distance from the point to the vertex is twice the distance from the point to the side.
While the meeting point of heights (or their extensions) is called orthocenter, the meeting of the internal bisectors is called center.
solved exercises
1) Epcar - 2016
A land in the shape of a right triangle will be divided into two lots by a fence made on the bisector of the hypotenuse, as shown in the figure.
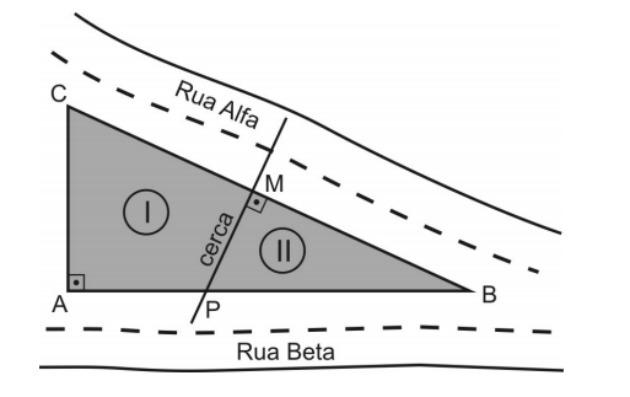
It is known that the sides AB and BC of this terrain measure, respectively, 80 m and 100 m. Thus, the ratio between the perimeter of lot I and the perimeter of lot II, in that order, is
To find the ratio between the perimeters, it is necessary to know the measurement of all sides of lot I and lot II.
However, we do not know the measurements of the sides ,
and
of lot I, nor the measure of
of lot II.
To start with, we can find the measure value on the side , applying the Pythagorean theorem, that is:
We could also find this value by noting that we have a multiple of the Pythagorean triangle 3, 4, and 5.
Thus, if one side measures 80 m (4. 20), the other measures 100 m (5. 20), so the third side can only measure 60 m (3. 20).
We know that the fence is the bisector of the hypotenuse, so it divides this side into two equal parts, forming a 90º angle with the side. In this way, the PMB triangle is a rectangle.
Note that triangles PMB and ACB are similar, as they have angles with the same measurement. calling the side of x, we have that side
will be equal to 80-x.
Therefore, we can write the following proportions:
We still have to find the measure on the side . To find this value, let's call this side y. By similarity of triangles, we find the following proportion:
Now that we know the measurement from all sides, we can calculate the perimeters of the lots:
Before calculating the perimeter of lot II, realize that the measurement of will be equal to
, i.e
. In this way, the perimeter will be:
Thus, the ratio between the perimeters will be equal to:
Alternative: d)
2) Enem - 2013
In recent years, television has undergone a real revolution, in terms of image quality, sound and interactivity with the viewer. This transformation is due to the conversion of the analog signal to the digital signal. However, many cities still do not have this new technology. Seeking to bring these benefits to three cities, a television station intends to build a new transmission tower, which sends a signal to antennas A, B and C, which already exist in these cities. The locations of the antennas are represented in the Cartesian plane:

The tower must be located at an equidistant location from the three antennas. The proper place for the construction of this tower corresponds to the coordinate point
a) (65; 35).
b) (53; 30).
c) (45; 35).
d) (50; 20).
e) (50; 30).
As we want the tower to be built in an equidistant location from the three antennas, it must be located at some point belonging to the bisector of the line AB, as represented in the image below:
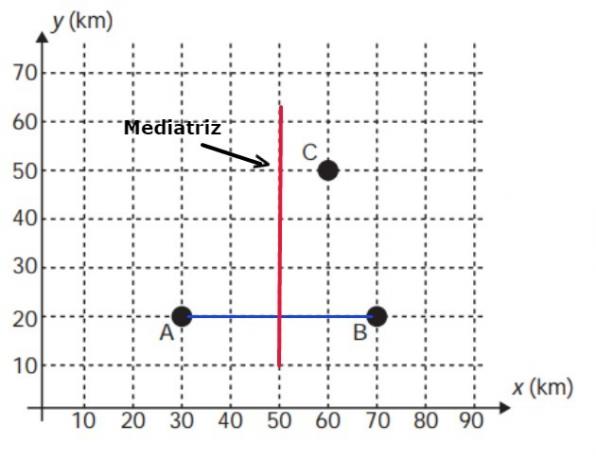
From the image, we conclude that the abscissa of the point will be equal to 50. Now we need to find the ordinate value. For this, let's consider that the distance between the AT and AC points are equal:
Alternative: e) (50; 30)
Read more about some related topics:
- Pythagorean theorem
- Line Segment
- Perpendicular Lines
- conical