Two distinct lines that are in the same plane are concurrent when they have a single point in common.
The concurrent lines form 4 angles to each other and, according to the measurements of these angles, they can be perpendicular or oblique.
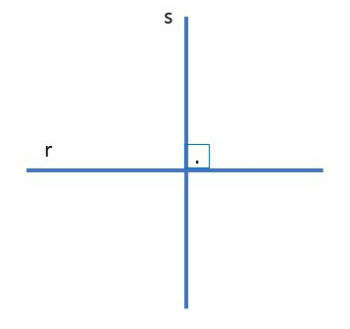
When the 4 angles formed by them are equal to 90º, they are called perpendicular.
In the figure below the lines r and s are perpendicular.
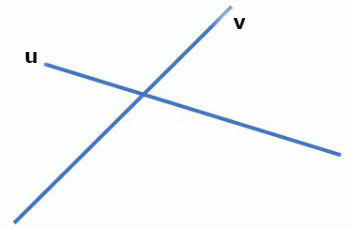
If the formed angles are different from 90º, they are called oblique competitors. In the figure below we represent the lines u and v obliques.
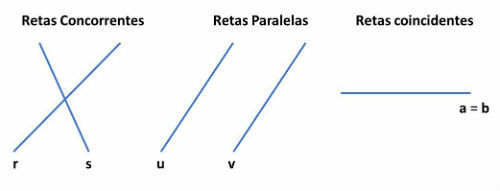
Competing, Coincident and Parallel Lines
Two lines that belong to the same plane can be concurrent, coincident or parallel.
While the concurrent lines have a single point of intersection, the coincident lines have at least two points in common and the parallel lines they have no common points.
Relative Position of Two Straights
Knowing the equations of two lines we can verify their relative positions. For this we must solve the system formed by the equations of the two lines. So we have:
- Concurrent lines: the system is possible and determined (a single point in common).
- Coincident lines: the system is possible and determined (infinite point in common).
- Parallel lines: the system is impossible (no common points).
Example:
Determine the relative position between the line r: x - 2y - 5 = 0 and the line s: 2x - 4y - 2 = 0.
Solution:
To find the relative position between the given lines, we must calculate the system of equations formed by their lines, so we have:
When solving the system by addition we find the following equation 0y = - 8, as there is no solution for this equation, it is impossible. In this way, the two lines are parallel.
Opposite Angles by Vertex
Two competing lines form two pairs of angles. These angles have a common point which is called a vertex.
The pairs of angles that are opposite by the vertex are congruent, that is, they have the same measurement.
In the figure below, we represent the angles AÔB and CÔD that are opposite by the vertex, as well as the angles AÔC and BÔD.

Intersection point between two concurrent straight lines
The intersection point between two concurrent lines belongs to the equations of the two lines. In this way, we can find the coordinates of this point in common, solving the system formed by the equations of these lines.
Example:
Determine the coordinates of a point P common to the lines r and s, whose equations are x + 3y + 4 = 0 and 2x - 5y - 2 = 0, respectively.
Solution:
To find the coordinates of the point, we must solve the system with the given equations. So we have:
Solving the system, we have:
Substituting this value in the first equation we find:
Therefore, the coordinates of the intersection point are , i.e
.
Learn more by also reading:
- Perpendicular Lines
- straight
- conical
Solved Exercises
1) In an orthogonal axis system, - 2x + y + 5 = 0 and 2x + 5y - 11 = 0 are, respectively, the equations of the lines r and s. Find the coordinates of the intersection point of r and s.
P (3, 1)
2) What are the coordinates of the vertices of a triangle, knowing that the equations of the support lines of its sides are - x + 4y - 3 = 0, - 2x + y + 8 = 0 and 3x + 2y - 5 = 0 ?
A (3, - 2)
B (1, 1)
C (5, 2)
3) Determine the relative position of the lines r: 3x - y -10 = 0 and 2x + 5y - 1 = 0.
The lines are concurrent, being the point of intersection (3, - 1).