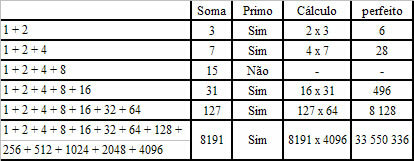
The motivation for the study of operations between sets comes from the ease they bring to solving everyday numerical problems. We will use some graphical tools, such as the venn diagram-Euler, to define the main operations between two or more sets, namely: union of sets, intersection of sets, difference of sets and complementary set.
union of sets
The union between two or more sets will be a new set made up of elements that belong to at least one of the sets in question. Formally, the union set is given by:

Let A and B be two sets, the union between them is formed by elements that belong to set A or set B.
In other words, just join the elements of A with those of B.

Example:
a) Consider the sets A = {0, 2, 4, 6, 8, 10} and B = {1, 3, 5, 7, 9, 11}:
A U B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
b) A = {x | x is a natural even number} and B {y | y is a natural odd number}
The union of all natural evens and all natural odds results in the entire set of natural numbers, so we have to:
Do not stop now... There's more after the advertising ;)
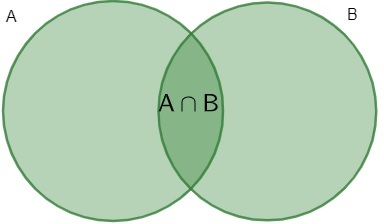
Intersection of sets
The intersection between two or more sets will also be a new set formed by elements that belong, at the same time, to all the sets involved. Formally we have:
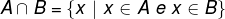
Let A and B be two sets, the intersection between them is formed by elements that belong to set A and set B. Thus, we must only consider the elements that are in both sets.
Example
a) Consider the sets A = {1, 2, 3, 4, 5, 6}, B = {0, 2, 4, 6, 8, 10} and C = {0, –1, –2, –3 }
A ∩ B = {2, 4, 6}
A ∩ C = { }
B ∩ C = {0}
The set that has no elements is called empty set and it can be represented in two ways.
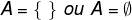
Read too: Set definition
difference of sets
The difference between two sets, A and B, is given by the elements that belong to A and no belong to B.

In the Venn-Euler diagram, the difference between sets A and B is:

Example
Consider the sets A = {0, 1, 2, 3, 4, 5, 6, 7}, B = {0, 1, 2, 3, 4, 6, 7} and C = { }. Let's determine the following differences.
A - B = {5}
A - C = {0, 1, 2, 3, 4, 5, 6, 7}
C - A = { }
Note that, in set A – B, we initially take set A and “take out” the elements from set B. In the set A – C, we take the A and “take out” the void, that is, no element. Finally, in C – A, we take the empty set and “take out” the elements from A, which, in turn, were no longer there.
Read too: Important notations about sets
Complementary sets
Consider sets A and B, where set A is contained in set B, that is, every element of A is also an element of B. The difference between the sets, B – A, is called the complement of A with respect to B. In other words, the complementary is formed by every element that does not belong to set A in relation to set B, in which it is contained.


Example
Consider the sets A = {0, 1, 2, 3, 4, 5} and B ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
The complement of A in relation to B is:

solved exercises
question 1 – Consider the sets A = {a, b, c, d, e, f} and B ={d, e, f, g, h, i}. Determine (A – B) U (B – A).
Solution
Initially we will determine the sets A – B and B – A and then we will perform the union between them.
A – B = {a, b, c, d, e, f} – {d, e, f, g, h, i}
A - B = {a, b,c}
B – A = {d, e, f, g, h, i} – {a, b, c, d, e, f}
B - A = {g, h, i}
Therefore, (A - B) U (B - A) is:
{a, b, c} U {g, h, i}
{a, b, c, g, h, i}
question 2 – (Vunesp) Suppose that A U B = {a, b, c, d, e, f, g, h}, A ∩ B = {d, e} and A – B = {a, b, c}, then:
a) B = {f, g, h}
b) B = {d, e, f, g, h}
c) B = { }
d) B = {d, e}
e) B = {a, b,c, d,e}
Solution
Alternative b.
Arranging the elements in the Venn-Euler diagram, according to the statement, we have:

Therefore, the set B = {d, e, f, g, h}.
by Robson Luiz
Maths teacher