You natural numbers were the first numerical set to be taken into account, historically. They emerged from the need to count of the human being. The set of natural numbers has as elements the positive numbers and integers, like 1, 2, 3, 4, …. This set has the addition operations, subtraction, multiplication, division, potentiation and radiciation.
What are natural numbers?
natural numbers are numbers strictly positive that do not have a comma, that is, they represent quantities whole. The set of natural numbers can be represented as follows:
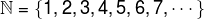
The set of natural numbers is a infinite set, that is, given any natural number, there is at least one number greater than it. See some examples of elements that belong and do not belong to this set.

From the example above, we have that the number 10, 2 and 100 belong to the natural set, and the numbers 1.65, –2 and 0 do not belong to the natural set.
Read too: Fun Facts About Dividing Natural Numbers
Successor of a natural number

As we said above, the set of natural numbers is an infinite set, that is, given any number no natural, there is always n+1, also natural. The number n+1 is called the successor of n. To determine the successor of any natural number, just add 1 to that number. As an example, let's determine the successors of the numbers 3, 1, 5 and 2p + 1.
The successor of the number 3 is given by 3+1, that is, the number 4. Similarly, the successors of 1 and 5 are, respectively, 2 and 6. Following the definition of successor, let's have that the successor of 2p + 1 is 2p + 1 + 1, that is, 2p + 2.
With the definition of successor, the idea that the set of natural numbers is infinite becomes clearer, since it is always possible to find any successor of a natural number.
Ancestor of a natural number
The predecessor of a natural number no is the one that precedes this number no. We can write the predecessor of no like n - 1. As an example, let's determine the predecessors of the numbers 2, 5, 1000 and 2p + 1.
The predecessor of 2 is given by 2 - 1, so it is the number 1. Similarly, the predecessors of 5 and 1000 are, respectively, the numbers 4 and 999. The predecessor of the number 2p + 1 is 2p + 1 – 1, that is, the predecessor of 2p +1 is the number 2p.
It is important to say that not every natural number has a predecessor, is the case of number 1. Applying the definition of ancestor, we have that the predecessor of the number 1 is 1 - 1 = 0, but the number zero does not belong to natural numbers. Therefore, every natural number has a predecessor, with the exception of number 1. For this reason, the number 1 is called the minimum element of the naturals, that is, it is the smallest natural number. We can write this information like this:

Subset of natural numbers
We know that the set of natural numbers is made up of strictly positive numbers, that is, numbers greater than zero. From the theory of sets, we have that, given the sets A and B, we say that B is a subset of A if every element of B is an element of A, that is, B is contained in A (B ⸦ A).
Thus, any set formed by natural numbers will be a subset of the natural numbers. See some examples:
Consider the sets:
A = {2, 4, 6, 8, 10, 12, …}
B = {1, 3, 5, 7, 9, 11, 13, …}
C = {2, 3, 5, 7, 11, 13, 17, 23}
D = {0, 1, 2, 3, 4, 5, 6, 7}
The sets A, B, and C are subsets of the natural numbers, as all the elements of these sets are also elements of the natural ones, that is, we can say that:
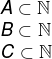
Now look at set D. Note that, in this set, not every element belongs to the set of natural numbers. This is the case with the number 0. Therefore, D it's not subset of natural numbers, that is, D is not contained in the set of natural numbers. We denote this fact as follows:
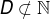
Read too: Prime numbers: what are they and how to find them?
even natural numbers
We say that a number is even if it is a multiple of the number 2, which is equivalent to saying that this number is divisible by 2. Look:
{2, 4, 6, 8, 10, 12, 14, 16, 18, 20,…}
Because the set of natural numbers is an infinite set, so is the set of even numbers. Also note that every element of the set of even numbers is also an element of the natural numbers and therefore the set of even numbers is a subset of the naturals..
Do not stop now... There's more after the advertising ;)
See that:
2 = 2 · 1
4 = 2 · 2
6 = 2 · 3
8 = 2 · 4
10 = 2 ·5
12 = 2 · 6
The set of even numbers can be obtained by multiplying all natural numbers by the number 2. So considering a natural number no, we can write an even number using the expression 2n, so the set of even numbers can be written in general by:
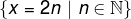
As an example, let's find out if the numbers 1000, 2098 and 55 are even.
Since 1000 = 2 · 500 and 2098 = 2 · 1049, they are even because there is a natural number that, multiplied by 2, gives them. Now, 55 is not even, as there is no natural number that, multiplied by 2, results in 55. Look:
54 = 2 · 27
56 = 2 · 28
As we well know, there is no natural number between 27 and 28, so 55 is not even.
Odd natural numbers
A number is odd if it is not even, that is, when it is neither multiple nor divisible by 2. Thus, the set of odd natural numbers are natural numbers that are not multiples of 2. This set can be written as follows:
{3, 5, 7, 9, 11, 13, 15, 17, 19, 21,…}
Analogously to what we did in the set of even numbers, we have:
3 = 2 · 1 + 1
5 = 2 · 2 + 1
7 = 2 · 3 + 1
9 = 2 · 4 + 1
11 = 2 · 5 + 1
13 = 2 · 6 + 1
The set of odd numbers can be obtained by multiplying all natural numbers by 2 and adding 1. considering a natural number no any, we can write any odd number using the expression 2n + 1. Generally speaking, we represent the set of odd numbers by:
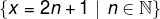
Note that the set of odd numbers is also an infinite set, since to get the odd numbers we multiply the natural numbers by 2 and then add 1. For this reason, the set of odd numbers is also a subset of naturals., because every element of this set is also an element of the natural ones.
See too: Even and odd number properties
solved exercises
question 1 – List only the natural numbers of the numbers listed below:
0, 1, 2, 0,43; -1, - 0.5 and 98,765
Solution
We know that the set of natural numbers is made up of strictly positive numbers that do not have a comma, so the natural numbers in the list are: 1, 2 and 98,765.
question 2 – Considering the general form of an even number, is it true that, adding two even numbers, the result is still even? The same goes for odd numbers?
Solution
We know that an even number can be written in general by multiplying any natural number by 2. Consider two distinct natural numbers, 2n and 2m, where m and no any natural numbers, the sum of the two is determined by:
2n + 2m
Putting the number 2 in evidence, we have:
2 ·(n+m)
Like no and m are two natural numbers, their sum is also, so n + m = k, where k a natural number.
2 ·(n+m)
2 · k
Therefore, the sum of two even natural numbers is also an even number, as the sum resulted in a multiple of 2.
Now we know that an odd number is given by multiplying a natural number by 2 added to the number 1. Now consider two distinct odd numbers, 2n +1 and 2m + 1, with m and no natural. Adding these numbers together, we have:
2n+1 + 2m +1
2n + 2m +2
Again putting the number 2 in evidence, we have:
2 (n+m+1)
Note that n + m + 1 is a natural number and we can represent it by p, that is, n + m + 1 = p, soon:
2 ·(n+m+1)
2 · P
Note that the result of adding two odd numbers resulted in a multiple of 2, that is, even. Therefore, the sum of two odd numbers is an even number.
Question 3 - (Tender / Pref. from Itaboraí) The quotient between two natural numbers is 10. By multiplying the dividend by 5 and reducing the divisor by half, the quotient of the new division will be:
a) 2
b) 5
c) 25
d) 50
e) 100
Solution
According to the statement, the quotient (division) between two natural numbers is 10. As we still don't know what these numbers are, let's name them by m and no, then:

Now, multiplying the dividend by 5 and reducing the divisor by half, we have:
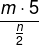
Carrying out the fraction division and replacing the value of m, we will have:

Reply: Alternative e.
by Robson Luiz
Maths teacher


