We say that a natural number is perfect if it is equal to the sum of all its factors (divisors), excluding itself. For example, 6 and 28 are perfect numbers, see:
6 = 1 + 2 + 3 (factors of 6: 1, 2, 3 and 6), we exclude the number 6.
28 = 1 + 2 + 4 + 7 + 14 (factors of 28: 1, 2, 4, 7, 14, 28), we exclude the 28.
Mersenne numbers are those in the form Mn = 2n – 1. He even thought that this expression would be able to calculate possible primes considering n = primes, but later it turned out that he was almost right. For example:
M1 = 21 – 1 = 1
M2 = 22 – 1 = 3 → n = 2 (cousin), M2 = 3 (cousin)
M3 = 23 – 1 = 7 → n = 3 (cousin), M3 = 7 (cousin)
M4 = 24 – 1 = 15
M5 = 25 – 1 = 31 → n = 5 (cousin), M5 = 31 (cousin)
M6 = 26 – 1 = 63
M7 = 27 – 1 = 127 → n = 7 (cousin), M7 = 127 (cousin)
M8 = 28 – 1 = 255
M9 = 29 – 1 = 511
M10 = 210 – 1 = 1023
M11 = 211 – 1 = 2047 → n = 11 (cousin), M11 = 2047 (not prime)
M13 = 213 – 1 = 8191 → n = 13 (cousin), M13 = 8191 (cousin)
Within the sequence of prime numbers there are elements that applied in the Mersenne formula do not generate prime elements, for example the number 11, when applied to the formula resulted in 2047, a number not cousin.
The knowledge of perfect numbers is attributed to Euclid, the famous Greek mathematician who founded Geometry. The method he uses starts with 1 adding powers of 2 to a prime. A perfect number is then obtained by multiplying the sum by the last power of 2.
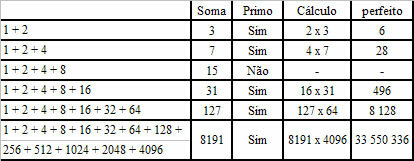
Note the relationship between the perfect number and the Mersenne prime numbers.
Do not stop now... There's more after the advertising ;)
by Mark Noah
Graduated in Mathematics
Brazil School Team
Numerical sets - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Mersenne, Prime Numbers and Perfect Numbers"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/mersenne-numeros-primos-numeros-perfeitos.htm. Accessed on June 27, 2021.

