THE formula of productFromterms of a geometric progression (PG) is a mathematical formula used to find the result of the multiplication between all the terms of a PG and is given by the following expression:
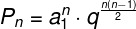
In this formula, Pno it's the productFromterms gives PG, a1 is the first term and is high The no in the formula. Furthermore, what and the reason of PG and no is the number of terms that will be multiplied.
As the number of terms to be multiplied is finite, so this formula it's just valid To the no first terms of PG or for progressionsgeometricfinite.
See too: Sum of terms of a finite PG
solved exercises
Exercise 1
calculate the productFromterms from PG (2, 4, 8, 16, 32, 64, 128).
Note that this PG has 7 terms, the first one is 2 and the ratio is also 2, because 4: 2 = 2. Replacing these values in the formula of the product of the terms of PG, we will have:
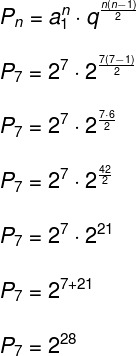
The last step, where we write 27 + 21 = 228, was made through the potency properties.
Do not stop now... There's more after the advertising ;)
Exercise 2
Determine the productFromterms of the following finite PG: (1, 3, 9, … 2187).
THE reason of this PG is 3: 1 = 3, your firstterm is 1, your last term is 2187, but the number of terms it has is unknown. To find it, you will need to use the formula from general term of PG, present in the image below. Substituting the known values in this formula, we will have:
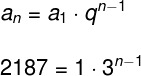
Like 2187 = 37, we will have:

As the bases of potencies obtained are equal, we can equal their exponents:

So, the number in terms of this PG is 8. Replacing reason, first term and number of terms in the formula of productFromterms from PG, we will have:
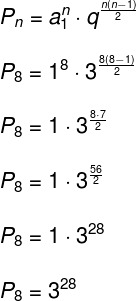
See too: Sum of terms of an infinite PG
By Luiz Paulo Silva
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "Product of the terms of a PG"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/produto-dos-termos-uma-pg.htm. Accessed on June 29, 2021.