You parallelograms are polygons of plane geometry widely explored for being common geometric figures in our daily lives. We define a parallelogram as a polygon that has opposite sides parallel, a characteristic that results in exclusive properties.
The particular cases of parallelograms are the squares, rectangles and diamonds. For each of these polygons, there are specific formulas for calculating area and perimeter.
Read too: Circle and circumference - geometric shapes with many features
Elements of a parallelogram
To be a parallelogram, the polygon must have opposite sides parallel. As specific features, we have to:
Every parallelogram is composed of four sides, and the opposite sides are parallel.

Every parallelogram has four internal angles, and the sum of these angles is always equal to 360º.

Every parallelogram has two diagonals.

Remember that parallelograms are particular cases of quadrilaterals, so there are features that are inherited from these geometric figures, such as the existence of two diagonals, four sides and four angles, as well as the sum of the inner and outer angles is always equal to 360º.
Properties of a parallelogram
1st property: Opposite sides of a parallelogram are congruent, that is, they have the same measure.

2nd property: Opposite angles of a parallelogram are congruent, and two consecutive angles are always supplementary (the sum equals 180°).
Knowing that AB and CD are parallel, then sides BC and AD are transverse to AB and CD; consequently, the angles formed (w and x) are supplementary as they are internal collateral angles. Furthermore, it is possible to demonstrate that angles x and z are congruent.


- 3rd property: The diagonals of a parallelogram are cut in half.
When we draw the two diagonals of a parallelogram, their meeting point divides each into its midpoints.

AM = CM
BM=DM
See too: Point, Line, Plane and Space: Basic Concepts of Geometry
Area of a parallelogram
The area of a parallelogram, in general, is calculated by the product of the base and the height. There are particular cases (rectangles, diamonds and squares) that have specific formulas – they will be presented throughout this text – but that arise from the general form.

A = b.h
b: base
h: height
Perimeter of a parallelogram
O perimeter is given by sum from all sides. As a parallelogram generally has two equal sides, its perimeter can be determined by:

P = 2 (a + b)
Special cases of parallelograms
As we know, by definition, in order to be a parallelogram, the polygon must have parallel sides. There are three quadrilaterals that are treated as particular cases of the parallelogram: the rectangle, the diamond and the square.
Square
we call square a four-sided polygon that has four sides and four congruent angles – each angle is exactly 90 degrees. Since the square is a parallelogram, all properties are valid for the square.

The area of a square and its perimeter are calculated similarly to what is done with a parallelogram, but since all sides of the square are equal, we can represent the area and perimeter of the square like this:
A=l²
P = 4.1
Rectangle
O rectangle it is a parallelogram that has all congruent angles. It gets this name because all your angles are straight, that is, the four angles measure 90º. The rectangle area is identical to the parallelogram area, but we can treat the vertical side as the height, after all, it is perpendicular to the base.

A=a.b
P= 2 (a + b)
Diamond
O diamond it is a parallelogram that has all its sides congruent. Note that there is no restriction on the angles, they can be different or not. Differently from the previous examples, the calculation of the area of a diamond is based on its diagonals. There is also a very important relationship between the diagonals of the diamond and its side.

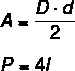
D: larger diagonal
d: minor diagonal
l: side
Given any diamond, we know that the diagonals intersect at the midpoint, forming four right triangles. Analyzing one of these triangles, it is possible to see a Pythagorean relationship between the side and half of each of the diagonals.
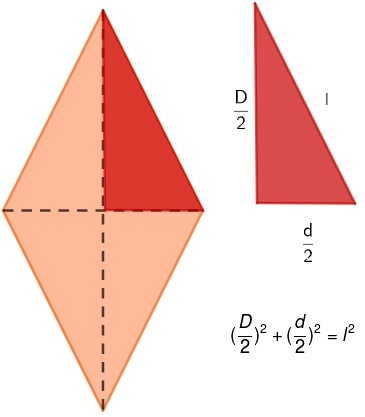
Also access: circumference length and circle area
Relationship between parallelograms
It is important to understand the definition of the parallelogram well, in order to avoid complications during classification. It's always good to remember that every parallelogram is a quadrilateral, but not every quadrilateral is a parallelogram.
We can also state that every rectangle, every square and every rhombus are parallelograms. Furthermore, comparing the special cases of parallelograms, we can see another relationship, because the square it has congruent angles, which is the definition of rectangle, and also congruent sides, which is the definition of diamond. As a consequence, we can say that every square is a rectangle and also a diamond.

solved exercises
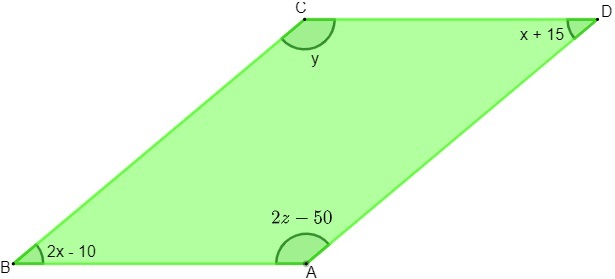
Question 1 - Knowing that the figure below is a parallelogram, what will be the value of x, y and z respectively?
a) 40,140 and 180
b) 30, 100 and 100
c) 25, 140 and 95
d) 30, 90 and 145
e) 45, 55 and 220
Resolution
1st step: Using the parallelogram property, we know that opposite angles are equal. When analyzing the image, it is more convenient to use this property at vertex angles B and D, as they have the same unknown.
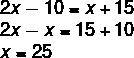
2nd step: Knowing that consecutive angles are supplementary and that x = 25, it is possible to find the value of y.

3rd step: Since the angles of vertices C and A are opposite, they are congruent, so we can find the value of z.
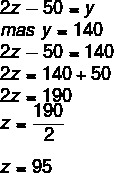
Alternative C.
Question 2 - Calculate the parallelogram area (sides measured in centimeters) below.
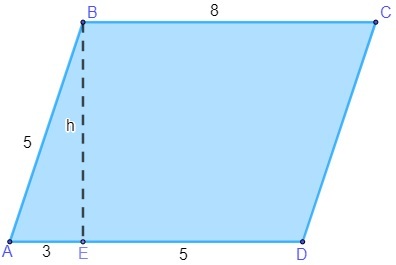
a) 16 cm²
b) 32 cm²
c) 8 cm²
d) 64 cm²
e) 40 cm²
Resolution
To find the area of the parallelogram, it is first necessary to find the value of h. Note that triangle AEB is hypotenuse rectangle equal to 5, so we can apply Pythagoras' theorem to find the value of h.
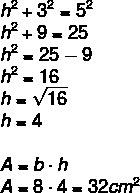
Alternative B.
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/paralelogramos.htm

