O principlegivesuncertainty, also called the Heisenberg uncertainty principle, was first stated in 1927, by the german physicist WernerHeisenberg (1901-1976). This principle indicates that it is not possible to measure, simultaneously and with accuracy, directly related quantities, such as velocity and position of a body.
Lookalso: Aspects of Quantum Theory
Uncertainty Principle Summary
The uncertainty principle relates two quantities, such as position and momentum or energy and time, through the product of the uncertainties of the measurements performed on them.
According to the uncertainty principle, the more accurate the position of a body, the less accurate the measurement of its momentum.
The uncertainty principle states that it is impossible for us to know, with complete precision and at the same time, two related physical quantities, also called canonically conjugate quantities.
What is the Heisenberg Uncertainty Principle?
O Heisenberg's Uncertainty Principle is a strange theoretical result obtained through calculations in the area of
Quantum Mechanics, whose basis is exactly this principle. Through knowledge of Classical Physics, it was believed that, knowing the starting position and speed, more specifically the amount of movement, of a body or a system of bodies, it would be possible to predict its behavior in the future moments. In this way, it would be possible to calculate positions later, determining its trajectory, values of acceleration,velocity,energy, etc. However, the uncertainty principle shows that even if we had the morenecessary of the measuring instruments at hand, it would not be possible for us to know, simultaneously and with accuracy, greatness like position and the amountinmovement orenergy and breakintime of the same body.Lookalso: Quantity of movement
So, according to that principle, if we can determine the position of a body with total precision, we will completely lose the measure of its the amountinmovement, since the imprecision about it will be considered infinite. Likewise, if we can be sure about the amount of movement of a body, it will not be possible to know its position.
The same goes for the greats energy and time: if we know exactly the amount of energy in a particle, we will lose precision in time measurements. Likewise, if we know how long it took for an event to occur with a particular particle, we would totally lose information about the amount of energy present in it.

Due to the uncertainty principle, it is impossible for the lowest energy level of a body to be zero.
Lookalso: What is energy?
Not all physical quantities are related to each other for their degree of precision. It is possible, for example, to determine the energy and the position of a particle without the precision of these measurements being inverselyproportional each other.
In addition, the uncertainty principle imposes that the product of the uncertainties of two quantities, such as position and momentum, will always be greater than or equal to Planck's constant (h) divided by 4π. It is common, however, to see the equation of the uncertainty principle written in terms of Planck's constant reduced (? = h/2π).
Heisenberg's Uncertainty Principle, which relates to uncertaintygivesposition of a body with the uncertainty of its momentum, is defined through the equation below:
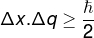
Δx – position uncertainty (m)
q – uncertainty of momentum (m/s)
? – reduced Planck constant (1.0545.10−34 J.s)
The uncertainty principle is also applied to the energy and time span of a body. Watch:

ΔAnd -uncertainty in energy (J)
t -uncertainty in time(s)
Suppose, for example, that, in a given experiment, you want to measure the position of an electron. In order to be able to measure its position, it is necessary that, somehow, a photon is emitted towards this electron. However, when the photon is reflected back to the observer, the electron recoils, as the photon transfers to it a small amount of motion directly proportional to its frequency. If we want to more accurately determine the position of this electron, we can increase the frequency of the photon. However, if we do this, we will increase the amount of motion given to the electron, thus losing the precision in measuring this magnitude.
Lookalso: What is string theory?
Solved exercise on the uncertainty principle
An extremely accurate laboratory measurement is able to determine the position of a molecule with uncertainties in the order equal to ± 10-15 m. According to the uncertainty principle, what is the smallest possible uncertainty in measuring the momentum of this molecule?
Resolution
The uncertainty principle states that the product of the position and momentum uncertainties must be greater than or equal to half of the reduced Planck constant:

Thus, taking the modulus of the position uncertainty (Δx = 10-15) provided by the exercise and the reduced Planck constant module (? = 1,0545.10−34 J.s), we will have to:

The above result indicates that, even if the laboratory has some instrument capable of measuring the amount of movement of this particle with errors smaller than 10-20 m, it will not be possible to measure its value accurately. Thus, we will always have the value calculated above as a plus or minus deviation.
By Me. Rafael Helerbrock
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/fisica/o-que-e-principio-incerteza.htm
