You numerical sets are groupings of numbers that separate them according to their most important characteristics and also taking into account their creation process. The set of irrational numbers is the one whose elements are decimal numbers that cannot be the result of division between two whole numbers. This definition is the opposite of the definition of rational number: any number that can be written in the form of fraction.
Brief history
Rational numbers were created from the need to divide objects between people. Later, the number line, where each point matches a single real number. Upon analyzing it more deeply, the mathematicians realized that there were “holes” in the number line and that there were no rational numbers that related to these points. There was initially a suspicion that there were many more numbers than just rational numbers (set that contains natural and integer numbers).
Over time, it was realized that these gaps should be filled with infinite decimal numbers and not periodic ones. Little by little it was also realized that some of these decimals could be represented by
roots not exact.Representation of irrationals on the number line
Draw a square of side 1, with one of the vertices at the origin of a number line, and calculate its diagonal measurement by Pythagorean theorem:
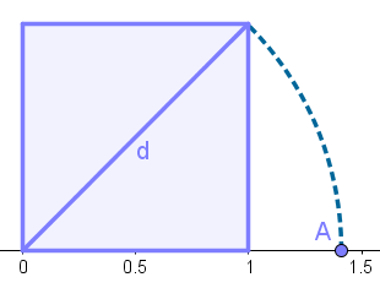
Calculating the diagonal of square side 1 to represent the irrational number √2
d2 = 12 + 12
d2 = 1 + 1
d2 = 2
d = √2
Knowing that the diagonal of this square measures √2, just use a compass to “transport” this measure to the number line. Just below the square, place the fixed end of the square at the beginning of the diagonal and the movable end at the end. Rotate the compass, marking where this end meets the number line.
Which numbers are irrational?
You irrational numbers are those who are not rational. Thus, its representatives are:
All non-recurring infinite decimals
Note that the number below is not periodic, but can be said to go on infinitely.
1,2345678910111213141516171819202122...
Some of these numbers can be represented by inexact roots and others are so important that they have been given a “name”.
Remarkable irrational numbers
Within the set of irrational numbers there are some elements that were used by great mathematicians in antiquity. We will highlight here just two of them: π and φ.
The irrational number π is obtained from the result of the division between the length and the diameter of a circle and represents the number starting with the following decimal places:
3,14159265358979...
Since this number has infinitely many decimal places and is not a periodic decimal, it is irrational.
The golden number, represented by the Greek letter φ, refers to the perfect proportion and is proportional to:
1 + √5
2
Thus, the number φ = 1.6180339... is also a irrational number.
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-conjunto-dos-numeros-irracionais.htm
