Trigonometric relationships are restricted to situations involving right triangles only.
In the situation below, PÔR is an obtuse-angled triangle, so we cannot use the known trigonometric relations. For situations like this, we use the law of sines or the law of cosines, as appropriate.
It is important to know that:
sin x = sin (180º - x)
cos x = - cos (180º - x)
sins law
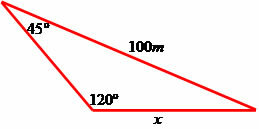
Solving the situation in Figure 1, we have:
We will apply the law of sines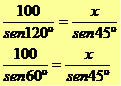
By the table of trigonometric ratios: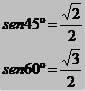
cosine law
a² = b² + c² - 2*b*c*cosA
b² = a² + c² - 2*a*c*cosB
c² = a² + b² - 2*a*b*cosC
Example
Review the diagram below:
If we choose to pump water directly to the house, how many meters of pipe would it take?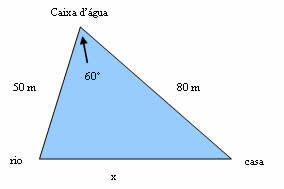
x² = 50² + 80² - 2*50*80*cos60º
x² = 2500 + 6400 - 8000*0.5
x² = 8900 - 4000
x² = 4900
x = 70 m
70 meters of pipe would be used.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Trigonometry - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/trigonometria-num-triangulo-qualquer.htm
