Complementary angles are angles that together add up to 90º. In a right angle divided into two parts, each represents a complement to the other.
In the image below, angle AÔC (60º) complements angle CÔB (30º). At the same time, the opposite occurs, that is, angle CÔB complements angle AÔC.

AÔC + CÔB = 90º
How to Calculate?
To calculate the measure of a complementary angle, we subtract 90° by its complement:
A + B = 90º
A = 90º - B
B = 90º - A
Examples:
1. Calculate the complementary angle knowing that one of them is 37°.
A + B = 90º
37th + B = 90th
B = 90 - 37th
B = 53rd
2. Angles A and B are complementary. Knowing that A = 60º, indicate how much the angle B is.
A + B = 90º
60º + B = 90º
B = 90º - 60º
B = 30th
Supplementary and Supplementary Angles
While the sum of the complementary angles is equal to 90°, the sum of the supplementary angles is equal to 180°.
Complementary angles, in turn, are those whose sum equals 360º.
And what are Adjacent Angles?
Adjacent angles are angles that have a common side and no common interior points. Adjacent angles can be complementary. This happens when these angles together measure 90°.
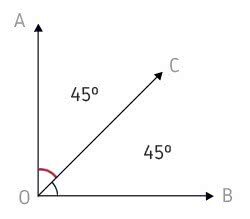
AÔC + CÔB are Complementary Adjacent Angles
Read too
- angles
- Rectangle Triangle
- Remarkable Angles
Exercises
1. Calculate the complement of the 53° angle.
A + B = 90º
53rd + B = 90th
B = 90º - 53º
B = 37th
2. Indicate the measure of the complementary angles such that one is triple the other.
22.5° and 67.5°
3. Two angles are complementary adjacent. Knowing that the measure of the largest angle is 47°, what is the measure of the smallest angle?
43º