The prism volume is calculated by multiplication between base area and height.
The volume determines the capacity that a spatial geometric figure has. Remember that it is usually given in cm3 (cubic centimeters) or m3 (cubic meters).
Formula: How to Calculate?
To calculate the prism volume, the following expression is used:
V = AB.H
Where,
THEB: base area
H: height
Note: Do not forget that to calculate the base area it is important to know the shape that the figure presents. For example, in a quadrangular prism the base area will be a square. In a triangular prism, the base is formed by a triangle.
Did you know?
The parallelepiped is a square-based prism based on parallelograms.
Read too:
- Prism
- Polyhedron
- Polygons
- Parallelogram
- Paving stone
- Spatial Geometry
- Geometric solids
Principle of Cavalieri
The Cavalieri Principle was created by the Italian mathematician (1598-1647) Bonaventura Cavalieri in the 17th century. It is still used today to calculate areas and volumes of geometric solids.
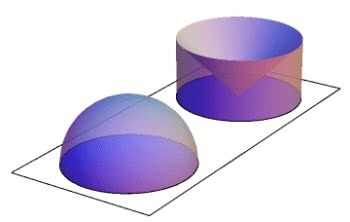
The statement of the Cavalieri Principle is as follows:
“Two solids in which every secant plane, parallel to a given plane, determines surfaces of equal areas are solids of equal volume.”
According to this principle, the volume of a prism is calculated as the product of the height and the base area.
Example: Solved Exercise
Calculate the volume of a hexagonal prism whose base side measures x and its height 3x. Note that x is a given number.
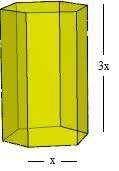
Initially, let's calculate the area of the base and then multiply it by its height.
For this, we need to know the apothema of the hexagon, which corresponds to the height of the equilateral triangle:
a = x√3/2
Remember that the apothema is the straight line that starts from the geometric center of the figure and is perpendicular to one of its sides.

Soon,
THEB= 3x. x√3/2
THEB = 3√3/2 x2
Therefore, the prism volume is calculated using the formula:
V = 3/2 x2 √3. 3x
V = 9√3/2 x3
Entrance Exam Exercises with Feedback
1. (EU-CE) With 42 cubes with 1 cm of edge we form a parallelepiped whose base perimeter is 18 cm. The height of this parallelepiped, in cm, is:
a) 4
b) 3
c) 2
d) 1
Answer: letter b
2. (UF-BA) Regarding a regular pentagonal prism, it is correct to state:
(01) The prism has 15 edges and 10 vertices.
(02) Given a plane that contains a side face, there is a line that does not intersect that plane and contains a base edge.
(04) Given two lines, one containing a side edge and the other containing a base edge, they are concurrent or reverse.
(08) The image of a side edge rotated 72° around the straight line passing through the center of each base is another side edge.
(16) If the base side and the prism height measure, respectively, 4.7 cm and 5.0 cm, then the lateral area of the prism is equal to 115 cm2.
(32) If the volume, base side and prism height measure, respectively, 235.0 cm3, 4.7 cm and 5.0 cm, so the radius of the circumference inscribed at the base of this prism measures 4.0 cm.
Answer: V, F, V, V, F, V
3. (Cefet-MG) From a rectangular pool 12 meters long and 6 meters wide, 10 800 liters of water were removed. It is correct to say that the water level has dropped:
a) 15 cm
b) 16 cm
c) 16.5 cm
d) 17 cm
e) 18.5 cm
Answer: letter a
4. (UF-MA) Legend has it that the city of Delos, in Ancient Greece, was being ravaged by a plague that threatened to kill the entire population. To eradicate the disease, the priests consulted the Oracle and the Oracle ordered the altar of the God Apollo to be doubled in volume. Knowing that the altar had a cubic shape with an edge measuring 1 m, then the value by which it should be increased was:
The) 3√2
b) 1
ç) 3√2 - 1
d) √2 -1
e) 1 - 3√2
Answer: letter c
5. (UE-GO) An industry wants to manufacture a gallon in the shape of a rectangular parallelepiped, so that two of its edges differ by 2 cm and the other one measures 30 cm. So that the capacity of these gallons is not less than 3.6 liters, the smallest of its edges must measure at least:
a) 11 cm
b) 10.4 cm
c) 10 cm
d) 9.6 cm
Answer: letter c