The Sphere in Spatial Geometry

THE Ball is a three-dimensional symmetrical figure that is part of spatial geometry studies.

A sphere is a geometric solid obtained by rotating the semicircle around an axis. It consists of a closed surface as all points are equidistant from the center (O).

Some examples of a sphere are the planet, an orange, a watermelon, a soccer ball, among others.

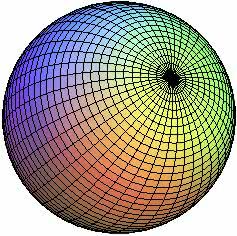
Sphere Components

• spherical surface: corresponds to the set of points in space in which the distance from the center (O) is equivalent to the radius (R).
• spherical wedge: corresponds to the part of the sphere obtained by rotating a semicircle around its axis.
• spherical spindle: corresponds to the part of the spherical surface that is obtained by rotating a semicircumference of an angle around its axis.
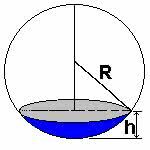
• spherical cap: corresponds to the part of the sphere (semisphere) cut by a plane.

To better understand the components of the sphere, review the figures below:

Sphere Formulas

See below for formulas to calculate the area and volume of a sphere:

Sphere Area

To calculate the spherical surface area, the formula is used:

THE_and = 4.п.r²

Where:

THE_and= sphere area
П (Pi): 3.14
r: lightning

Sphere Volume

To calculate the sphere volume, the formula is used:

V_and = 4.п.r³/3

Where:

V_and: sphere volume
П (Pi): 3.14
r: lightning

To learn more, read also:

• Spatial Geometry
• Geometric Shapes
• Geometric solids
• Pythagoras Theorem - Exercises

Solved Exercises

1. What is the area of ​​the sphere with radius √3 m?

To calculate the spherical surface area, use the expression:

THE_and=4.п.r²
THE_and = 4. п. (√3)²
THE_and = 12п

Therefore, the area of ​​the sphere with radius √3 m is 12 п.

2. What is the volume of the sphere with radius ³√3 cm?

To calculate the volume of the sphere, use the expression:

V_and = 4/3.п.r³
V_and = 4/3.п.(³√3)³
V_and = 4п.cm³

Therefore, the volume of the sphere of radius ³√3 cm is 4п.cm³.