Some situations involving geometric progressions receive special attention regarding development and solution. Certain geometric sequences, when added, tend to a fixed numerical value, that is, the introduction of new terms in the sum makes as the geometric series comes closer and closer to one value, this type of behavior is called a Geometric Series Convergent. Let's analyze the following geometric progression (4, 4/3, 4/9, 4/27, ...) of reason q = 1/3, determining the following situations: Y5 and S10.
Sum of Terms of a Geometric Progression
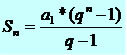

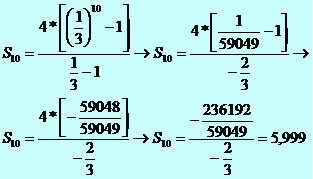
As the number of terms increases, the value of the sum of the terms in the progression approaches 6. We conclude that the sum of the sequence (4, 4/3, 4/9, 4/27, ...) converges to 6 whenever new elements are introduced. We can demonstrate the general situation as follows: 4 + 4/3 + 4/9 + 4/27 +... = 6.
Another situation involving Geometric Progressions is the Divergent Series, which do not tend to a number fixed as the Convergents, as they increase more and more as new terms are introduced to the progression. Watch the PG
(3, 6, 12, 24, 48, ...) of ratio q = 2, let's determine the sums when: n = 10 and n = 15.

Note that the sum increased with the number of terms, S10 = 3069 and S15 = 98301, so we say that the series diverges, it gets big as you want.
Returning to the study of Convergent Series, we can determine a single expression that expresses the value to which the geometric series approaches, for that we will consider some points. Let's assume that the ratio q assumes values within the range ] – 1 and 1[, that is – 1 < q < 1, thus, we can conclude that the element qn of the expression that determines the sum of terms of a PG tends to zero as the number of terms n increases. In this way, we can consider qn = 0. Follow the demo:
Do not stop now... There's more after the advertising ;)
sno = The1(qn – 1) = The1(0 – 1) = – The1 = The1
what – 1 q – 1 q – 1 1 – what
So, the following expression follows:
sno = The1, –1 < q < 1
1 – what
by Mark Noah
Graduated in Mathematics
Brazil School Team
Progressions - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Converging and Divergent Geometric Series"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/series-geometricas-convergentes-divergentes.htm. Accessed on June 29, 2021.