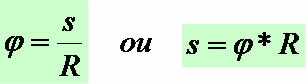THE Spatial Geometry studies geometric figures in space. Understand space as a place where we can find all geometric properties in more than two dimensions.
It is in early childhood (up to two years of age) that the child develops the perception of space. This process takes place in a multifaceted way, as the child conceives a collection of spaces, which, according to Piaget, are four: tactile, auditory, visual and oral space. It is only from two to seven years of age that the child recognizes space as something common, in which all spaces described above are included simultaneously.
We can represent space through the spatial projection of the three dimensions, which are: height, length and width. Cartesian coordinates are given by the x, y and z axes. Using point location, you can draw straight lines in space that form planes and define geometric shapes and structures.
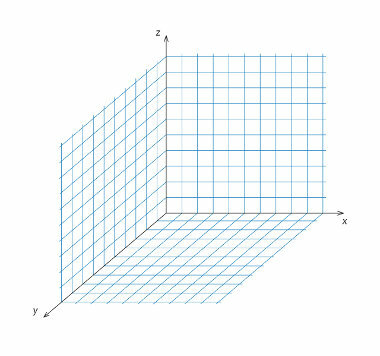
Another segment of Mathematics that makes up Spatial Geometry is Analytical Geometry. In the latter, the representation of an image in the spatial projection is given by vectors that have a modulus (positive numeric value), direction (horizontal or vertical) and direction (up, down, right or left). Space is also present when we study geometric solids, which are limited portions of space.
Do not stop now... There's more after the advertising ;)

Great scholars of Exact Sciences conceived and formalized studies related to Spatial Geometry. Among them, we can highlight: Pythagoras, Plato, Euclid, Leonardo Finonacci, Joannes Kepler, among others.
Spatial Geometry is present in the abstractions of Mathematics and in our everyday world. We realize its existence every day when we look at objects, structures and animals that are around us. When we perform this action, we can see the total volume rather than just the surface, which is a two-dimensional projection.
At school, Spatial Geometry is studied in the subject of Mathematics. The contents listed below are those taught in the classroom:
- The plane and the space;
- Prism volume;
- Sphere volume;
- Pyramid volume;
- Point, straight and plane relative positions;
- Relative positions of two lines;
- Relative positions of two planes;
- Perpendicularity between planes;
- Orthogonal projection;
- Euler relation;
- Polyhedra;
- Prisms;
- Cobblestones;
- Side area and total area of solids;
- Cylinder;
- Cone;
- Pyramid;
- Cone;
- Ball;
- Symmetry.
By Naysa Oliveira
Graduated in Mathematics