When we talk about the volume of a solid, we are referring to the capacity of that solid. We will see below how to calculate the volume of the paving stone, of cube It's from straight circular cone. It is worth noting that, when calculating the volume of a solid, it is necessary that all its measurements have the same notation. For example, if one of the measurements is in centimeters and the other is given in meters, it is necessary to transform one of them to make it equal to the others.
A rectangular parallelepiped is a six-sided solid that has flat, parallel rectangular faces. Try to imagine the cobblestone below as a swimming pool. If we want to know its capacity, it is like saying that we want to find out how much water it holds. To come up with an answer, we'll need to analyze some data for this solid, such as the width and length of the base rectangle, as well as the height or depth.

To calculate the volume of this parallelepiped, we must multiply the measures identified by a, b and c
Therefore, to calculate the volume of the parallelepiped, we have the following formula:
V = a. B. ç
If we consider a parallelepiped in which the width of the base measures 10 m, the length of the base, 5 m, and the height of the parallelepiped measures 8 m, we will have the following volume:
V = (10 m). (5 m). (8 m)
V = 400 m3
We have a special kind of rectangular parallelepiped, the cube—a solid with six square faces and the same lengths of sides. Below is a cube whose edges measure The.
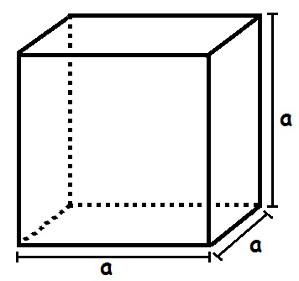
To calculate the cube's volume, we must multiply the measure of the edge raised by the third power.
To calculate the cube's volume, let's multiply the edges so that we'll make the third power of that edge:
V = a. The. The
V = a3
If we say, for example, that the edge of this cube measures 3 m, its volume will be:
V = (3m)3
v = 27 m3
Another solid that we will analyze is the straight circular cone. This solid has the characteristics of a circular base of radius. r, a height H, which forms a right angle with the base, and a generatrix g. The generatrix of a cone is the line segment that connects the top of the height to the ends of the base. In the following figure, we can more easily see each of these structures:

To calculate the volume of the straight circular cone, we must multiply the height by π and by the square of the radius, as well as dividing the result by 3
Do not stop now... There's more after the advertising ;)
To calculate the area of the straight circular cone, we will do:
V = ⅓ π.r2.H
Consider a cone whose base has a radius of 2 m and the height is 8 m. Consider π = 3,14. Let's calculate the volume of the cone:
V = ⅓ π.r2.H
V = 1 . 3,14. 22. 8
3
V = 3,14. 4. 8
3
V = 100,48
3
V ≈ 33.49 m3
So the volume of the cone is approximately 33.49 m3.
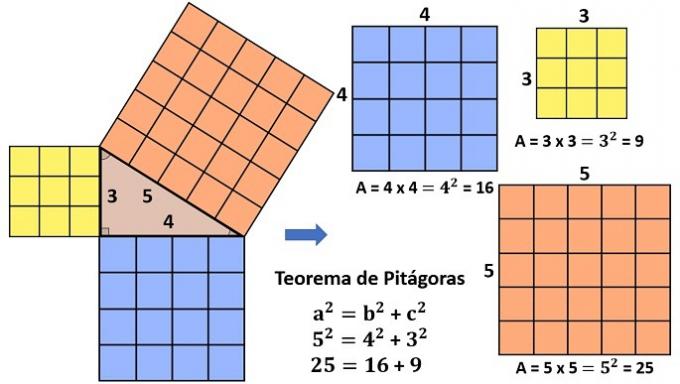
Suppose now that we have a straight circular cone where the generatrix measures 5 m and the height 4 m. To calculate the volume of this solid, we need to find the radius measure, for that, we will use the Pythagorean Theorem:
g2 = h2 + r2
r2 = g2 - H2
r2 = 52 – 42
r2 = 25 – 16
r2 = 9
r = 3 m
Now that we have the radius value, we can calculate the volume of the cone using the formula:
V = ⅓ π.r2.H
V = 1 . 3,14. 32. 4
3
V = 3,14. 9. 4
3
V = 113,04
3
V = 37.68 m3
Therefore, the volume of this straight circular cone is 37.68 m3.
By Amanda Gonçalves
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
RIBEIRO, Amanda Gonçalves. "Cobblestone, Cube and Cone Volume"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/volume-paralelepipedo-cubo-cone.htm. Accessed on June 27, 2021.