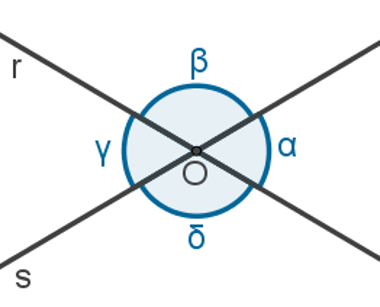
O angle is region delimited by two ray. To measure it, there are two possible units: degree or radian. According to its measurement, it can be classified into sharp, straight, obtuse or shallow.
When we have two angles, we can establish relationships between them. If they have the same measurement, they are called congruent. When the sum between them is equal to 90º or 180º or 360º, they are known, respectively, as angles. complementary, supplementary and complementary.
Read too: Remarkable angles – learn about the most used angles in trigonometry
How to measure an angle
For drawing or measuring an angle, in the plane geometry we use the compass it's the protractor. There are some other instruments used by construction professionals, such as the theodolite.
As the angle corresponds to the region that is between two ray, to perform the measurement on a protractor, we position one of the straight lines pointing to 0º and observe the degree to which the other straight line is pointed out.

angle measurement unit
There are two possibilities for measuring an angle: o degree it's the radian. 1 rad is the angle that makes the arc formed in the circumference have the same measurement as the radius of that circle.
It is quite common the need to convert degrees to radians. For this, we use rule of three, always knowing that 180º corresponds to π.
Example
- What is the value of an angle of 60° in radians?
Resolution:
π rad 180º
x rad 60º

Now, to convert from radians to degrees, just replace π by 180º.
Example
- What is the value of the angle that measures the third of 2π rad in degrees?
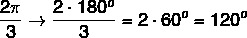
Do not stop now... There's more after the advertising ;)
angle classification
An angle can be classified according to its measurement. In addition to null (0° angle), an angle can be asharp, straight, obtuse, shallow, concave or whole.
Acute angle: when its measure is a number greater than 0 and less than 90º.
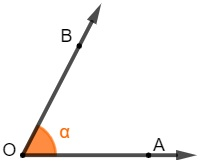
Note that angle AÔB, also represented by α, is an angle greater than 0º and smaller than 90º.
Straight angle: it has exactly 90º. When this happens, we can also say that the straight lines cross perpendicularly.
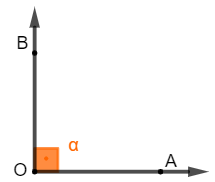
Usually the right angle has the angular region (orange region in the image) represented by a square.
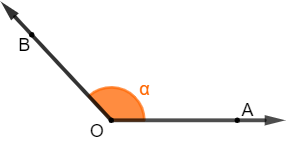
obtuse angle: when your measurement is greater than 90º and less than 180º.
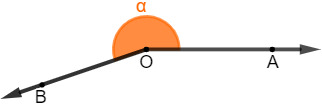
Shallow angle: also known as half-turn or half-moon, this angle is equivalent to half of a whole angle, so it is exactly 180º.

concave angle: less common in everyday situations than the others, it is the angle that measures greater than 180º and less than 360º.
Full angle: as the name suggests, this angle represents the complete turn, having exactly 360º.

Read too: Polygons - geometric figures formed by straight segments
congruent angles
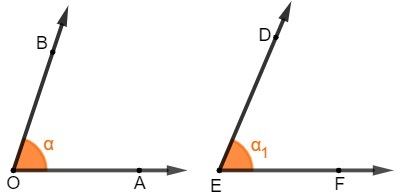
Two angles are called congruent when they have the same measurement. This concept is very confused with the idea of equality. In order for the angles to be congruent, they don't necessarily have to be equal, but need to have the same measurement.
Opposite skin vertex angles
A very common case of congruent angles is when the angles are opposed by the vertex. When we have two concurrent lines, that is, that intersect, it is possible to draw several angles between them. When we compare two angles that are on opposite sides of the same vertex, they will always be congruent, that is, they will have the same measurement.

Read too: Inner and Outer Side Angles
Bisector of an angle
We define as a bisector of an angle a semi-straight that divides the angle into two congruent parts, that is, of the same measure.
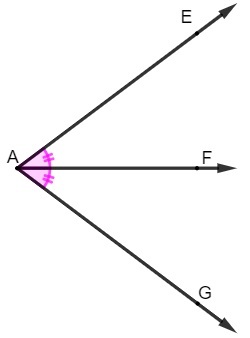
The bisector AF divides the largest angle EÂG into two congruent angles. Angle EÂF is congruent to angle FÂG.
Consecutive angles and adjacent angles
Two angles are consecutive when they have the same vertex and one of its sides in common. The concept of adjacent angle is often confused with that of consecutive angle, but they have a subtle difference – starting with the fact that adjacent angles are particular cases of angles consecutive.
Two consecutive angles are adjacent when they have only the side and vertex in common, but no region can belong to both at the same time.

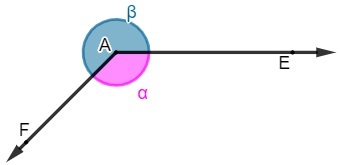
In the above representation, we can find consecutive angles and adjacent consecutive angles. The angles EÂG and EÂF are consecutive, as they have side EA and vertex A in common. Note that in this case the angle EÂF is contained within the larger angle EÂG, which makes them not adjacent.
The angles EÂF and FÂG are also consecutive, as they have the FA side in common and also the vertex A, however, in this case, they only have this in common, which makes them consecutive and adjacent.
Particular cases of sum of two angles
There are three particular cases for the sum between two angles, according to the result of that sum. They are: complementary angles, supplementary angles and complementary angles.
→ complementary angles
Two angles are known as complementary when the result of the sum of the two is equal to 90º, that is, together they form a right angle.

→ supplementary angles
Two angles are considered supplementary when The sum between them is equal to 180º, that is, together they form a shallow angle.

→ complementary angles
Less common than the previous ones in textbooks and tests, the complementary angle occurs when the sum of two angles generates an integer angle, that is, an angle of measurement equal to 360º.
Parallel lines cut by a transverse
when there are two parallel lines cut by a transverse, it is possible to establish an important relationship between the angles formed in the straight line. There are three important pieces of information that help you discover the value of all eight angles in this situation. Look:
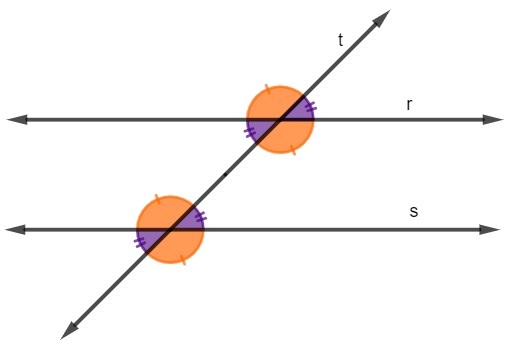
Acute angles are always congruent;
Obtuse angles are always congruent.
The sum of an acute with an obtuse is equal to 180º, that is, they are supplementary.
These three pieces of information allow us, through equations, to discover the value of all eight angles when there are two parallel lines cut by a transversal one.
Read too: Sine and Cosine of Supplementary Angles
solved exercises
Question 1 - (IFG) Assuming that a'//a and b'//b, mark the correct alternative.

a) x = 31° and y = 31°
b) x = 56° and y = 6°
c) x = 6th and y = 32nd
d) x = 28° and y = 34°
e) x = 34° and y = 28°
Resolution:
Analyzing the figure, we have two acute angles and two obtuse angles.
As the statement informs us that they are parallel lines cut by a transversal one, the acute and obtuse angles are congruent, so we have to:

Let 2x + y = 118º be equation I and x+y = 62º equation II, let's solve them by the method of addition, multiplying equation II by ( -1).
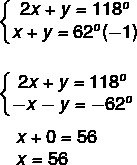
Knowing the value of x, let's substitute it into equation II.
x+y = 62º
56th + y = 62nd
y=62º - 56º
y = 6th
Alternative B.
Question 2 - Two angles are supplementary. Knowing that one is twice the other, what is the value of the smallest angle?
a) 120th
b) 90º
c) 180º
d) 60th
e) 30th
Resolution:
If these angles are supplementary, the sum equals 180°. So let x be the smallest, then the largest is 2x.

Alternative D.
By Raul Rodrigues de Oliveira
Maths teacher