Convex polygons are those with internal angles less than 180º. Polygons are flat, closed figures, formed by straight segments that connect at the vertices. In convex ones, all vertices point towards the outside.

Polygons receive special names, depending on the number of sides, such as triangles that have three sides or quadrilaterals with four sides.
When studying polygons, we can classify them into those that are convex and those that are not. Non-convex polygons are called concave.
How to recognize a convex polygon
There are two tests used to find out whether a polygon is convex. The first is to check if any of the internal angles are greater than 180º. If so, the polygon is not convex and is called concave.

Having an angle greater than 180º induces the effect of pointing inward, that is, it creates a concavity. Hence the name concave.
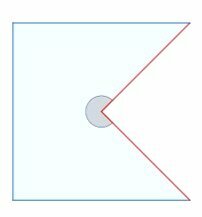
For example, this polygon has five sides and is not convex, that is, concave.
Examples of convex polygons.

A second way follows from the first and consists of drawing a segment inside the polygon. If it is possible to draw a segment between two internal points and part of it remains outside, the polygon is not convex.

Note that the segment connects two internal points of the polygon, leaving a part in the external region.
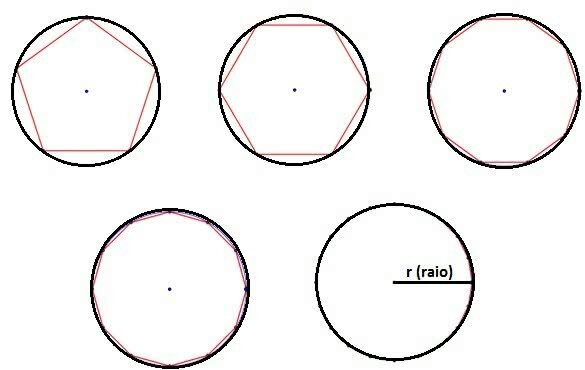
Regular and convex polygons
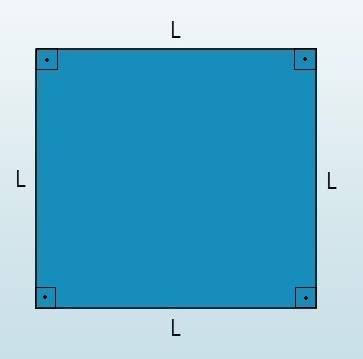
All the regular polygons are convex. A regular polygon is equilateral (all sides equal) and equiangular (all angles equal).
An example of a regular polygon is a square, which has four equal sides and therefore four equal angles.
Continue learning about polygons at:
- Polygons
- Exercises on polygons
- Area of polygons
- Sum of internal angles of polygons
ASTH, Rafael. Convex polygons: what they are and how to recognize one.All Matter, [n.d.]. Available in: https://www.todamateria.com.br/poligonos-convexos/. Access at:
See too
- Exercises on polygons
- Polygons
- Sum of the interior angles of a polygon
- Regular polygons: what they are, properties and examples
- Diagonals of a polygon: what they are and how to calculate them
- Polygon Area
- Area and Perimeter
- Math Lesson Plan: Area of Polygons and Circles (8th Grade)