How to Calculate the Square Area?

THE square area corresponds to the size of the surface of this figure. Remember that a square is a regular quadrilateral that has four congruent sides (same size).

In addition, it has four internal 90° angles, called right angles. Thus, the sum of the square's internal angles totals 360°.

Area Formula

To calculate the area of ​​the square, simply multiply the measure of two sides (l) of this figure. The sides are often called base (b) and height (h). In the square, the base is equal to the height (b=h). So, we have the formula for the area:

A = L²
or
A = b.h

Note that the value will usually be given in cm² or m². This is because the calculation corresponds to the multiplication between two measures. (cm. cm = c² or m. m = m²)

Example:

Find the area of ​​a 17 cm square.

H = 17 cm. 17 cm
H = 289 cm²

See also other articles on flat figure areas:

• Polygon Area
• Rectangle Area
• Triangle Area
• Circle Area
• Trapeze Area
• Diamond Area
• Flat Figure Areas
• Flat Figures Area - Exercises

Stay tuned!

Different from the area, the perimeter of a flat figure is found by summing all sides.

In the case of the square, the perimeter is the sum of the four sides, given by the expression:

P = L + L + L + L
or
P = 4L

Note: Note that the perimeter value is usually given in centimeters (cm) or meters (m). This is because the calculation to find the perimeter corresponds to the sum of its sides.

Example:

What is the perimeter of a square with a 10 m side?

P = L + L + L + L
P = 10 m + 10 m + 10 m + 10 m
P = 40 m

Learn more about the topic at:

• Area and Perimeter
• Square Perimeter
• Perimeters of Flat Figures

Square Diagonal

The square's diagonal represents the line segment that cuts the figure into two parts. When that happens what we have are two right triangles.

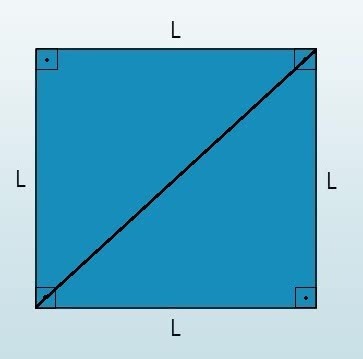
Right triangles are a type of triangle that has a 90° interior angle (called a right angle).

According to Pythagorean theorem the squared hypotenuse is equal to the sum of its squared legs. Soon:

THE² = b² + c²

In this case, “a” is the diagonal of the square that corresponds to the hypotenuse. It is the opposite side of the 90° angle.

The opposite and adjacent legs correspond to the sides of the figure. Having made this observation, we can find the diagonal through the formula:

d² = L² + L²
d² = 2L²
d = √2L²
d = L√2

So if we have the value of the diagonal we can find the area of ​​a square.

Solved Exercises

1. Calculate the area of ​​a square with a side of 50 m.

See Answer

A = L²
A = 50²
A = 2500 m²

2. What is the area of ​​a square whose perimeter is 40 cm?

See Answer

Remember that the perimeter is the sum of the four sides of the figure. Therefore, the side of this square equals ¼ of the total value of the perimeter:

L = ¼ 40 cm
L = ¼.40
L = 40/4
L = 10 cm

After finding the measure on the side, just put in the area formula:

A = L²
H = 10 cm .10 cm
H = 100 cm²

3. Find the area of ​​a square whose diagonal measures 4√2 m.

See Answer

d = L√2
4√2 = L√2
L = 4√2 / √2
L = 4 m

Now that you know the square's side measurement, just use the area formula:

A = L²
A = 4²
A = 16 m²

See also other geometric figures in the articles:

• plane geometry
• Rectangle
• Spatial Geometry
• Math Formulas