How to Calculate the Circle Area?

THE circle area corresponds to the surface value of this figure, taking into account its radius (r) measurement.

What is Circle?

It is worth remembering that the circle, also called a disk, is a geometric figure that is part of the studies of plane geometry.

This figure appears as the regular polygons inscribed on it increase the number of sides.

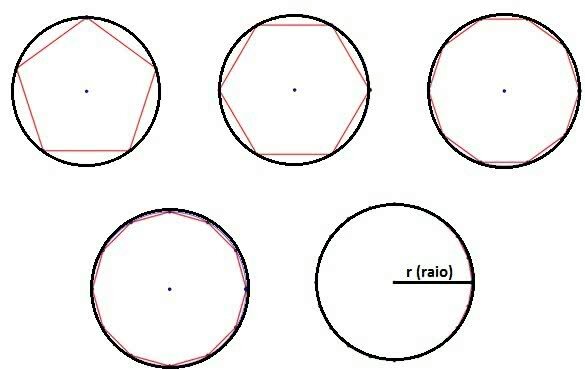
In other words, as the number of sides of the polygons increases, they get closer to the circular shape.

Learn more about plane geometry.

Formula: Circle Area Calculation

To calculate the area of ​​the circle we must use the following formula:

A = π. r²

Where,

π: constant Pi (3.14)
r: lightning

Stay tuned!

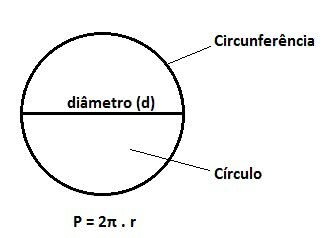
remember that the lightning (r) corresponds to the distance between the center and the edge of the circle.

already the diameter is a straight line segment that passes through the center of the circle, dividing it into two equal halves. That said, the diameter equals twice the radius (2r).

Learn more about pi number.

Circle Perimeter

A perimeter is a mathematical concept that measures the length (outline) of a given figure. In other words, perimeter is the sum of all sides of a geometric figure.

In the case of the circle, the perimeter is called circumference and is calculated by twice the radius measure (2r). Thus, the perimeter of the circumference is measured by the formula:

P = 2 π. r

Also read the articles:

• Area and Perimeter
• Circle Perimeter
• Perimeters of Flat Figures
• Polygon Area
• Flat Figure Areas
• Flat Figures Area - Exercises

Difference between Circle and Circumference

Although most people believe that the circle and circumference are the same figures, they do have differences.

While the circumference it is the curved line that bounds the circle, the circle is a flat figure bounded by the circumference.

Solved Exercises

1. Calculate the area of ​​a circle that has a radius of 3 cm.

See Answer

To calculate the area, just put the value in the formula:

A = π. r²
A = π. 3²
A = 9π cm²
A = 9. (3,14)
A = 28.3 cm²about

2. What is the area of ​​a circle whose diameter is 10 cm?

See Answer

First of all we must remember that the diameter is twice the radius value. Therefore, the radius of this circle measures 5 cm.

A = π. r²
A = π. 5²
A = π. 25
A = 25π cm²
A = 25. (3,14)
A = 78.5 cm²about

3. Determine the area of ​​a circle of length 12π cm.

See Answer

The length of the circle indicates its perimeter, that is, the value of the figure's outline.

First, we must use the perimeter formula to find the radius value of this circle.

P = 2 π. r
12 π= 2 π. r
12 = 2 π. r / π
12 = 2r
r = 6 cm

Soon, we find that the radius value of this circle is 6 cm. Now just use the area formula:

A = π. r²
A = π. 6²
A = π. 36
A = 36π cm²
A = 36. (3,14)
A = 113.04 cm² about