The diagonals in a polygon are straight segments that connect two non-consecutive vertices through their internal region.
Thus, to draw a diagonal, it is necessary to start at a vertex and continue with the line to another, which is not neighboring, since the segment must cut through the interior of the polygon. Note that if the line goes to a consecutive vertex, it becomes the side itself.
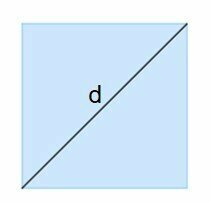
It is important to remember that a polygon is a flat closed figure, formed by consecutive straight segments that connect at the vertices, where the sides meet. It is these segments that form the sides that, depending on their quantity, will give the name of the polygon, such as: triangles, quadrilaterals, pentagons, etc.
Number of diagonals in a polygon
As a diagonal is a segment that connects two vertices, the greater the number of vertices, the greater the number of diagonals.
In a polygon the number of vertices is equal to the number of sides. Thus, a square has four sides and four vertices.
It is not possible to know the number of diagonals in every type of polygon, only the convex ones. These polygons, the convex ones, do not have concavity, they are those whose internal angles are less than 180º.
Number of diagonals formula: calculating the quantity in convex polygons
The number of diagonals in a convex polygon is calculated by the formula:
Where,
d is the number of diagonals,
n is the number of sides (which is equal to the number of vertices).
Note that (n - 3) is the number of diagonals that start from a single vertex. In a square, for example, only one diagonal starts from each vertex, since 4 - 3 = 1.
It is easy to see that a triangle has no diagonals, since n - 3 = 0. In a quadrilateral, we simply draw an “x” to verify that it has two diagonals.
This quantity is multiplied by the number of sides, or number of vertices, represented by the letter n. Since this causes a diagonal to be counted twice, we have to divide the result by two. Thus, we arrive at the formula.
How many diagonals does a pentagon have?
A pentagon is a polygon with five sides and therefore five vertices. Using the formula, we have:

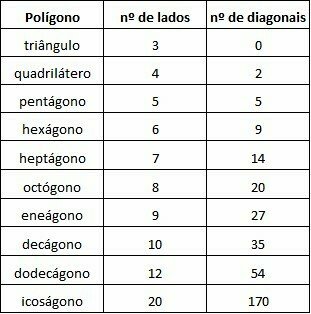
Table of polygons and their diagonals
Learn more with:
- Polygons
- Exercises on polygons
- Sum of the interior angles of a polygon
- Polygon Area
ASTH, Rafael. Diagonals of a polygon: what they are and how to calculate them.All Matter, [n.d.]. Available in: https://www.todamateria.com.br/diagonais-de-um-poligono/. Access at:
See too
- Exercises on polygons
- Sum of the interior angles of a polygon
- Polygons
- Regular polygons: what they are, properties and examples
- Polygon Area
- Convex polygons: what they are and how to recognize one
- Area and Perimeter
- Angles