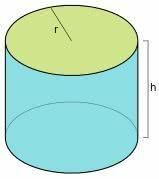
O cylinder volume is related to the capacity of this geometric figure. Remember that the cylinder or circular cylinder is an elongated, rounded geometric solid.
It has the same diameter along its entire length and has two bases: top and bottom. The bases are two parallel circles with radii of equal measure.
The radius of the cylinder is the distance between the center of the figure and the edge. Thus, the diameter equals twice the radius (d=2r).
Many cylindrical figures are present in our daily lives, for example: batteries, cups, soda cans, chocolate drinks, peas, corn, etc.
It is important to note that the prism and the cylinder are similar geometric solids, their volume being calculated by the same formula.
Formula: How to Calculate?
The formula for finding the volume of the cylinder corresponds to the product of the area of its base and the measurement of its height.
The cylinder volume is calculated in cm3 or m3:
V = AB.H or V = π.r2.H
Where:
V: volume
THEB: base area
π (Pi): 3.14
r: lightning
H: height
Want to know more about the topic? Read the articles:
- Cylinder
- Cylinder Area
- Spatial Geometry
Solved Exercises
1. Calculate the volume of a cylinder whose height measures 10 cm and the diameter of the base measures 6.2 cm. Use the value of 3.14 for π.
First, let's find the radius value of this figure. Remember the radius is twice the diameter. To do this, we divide the diameter value by 2:
6,2: 2 = 3,1
Soon,
r: 3.1 cm
h: 10 cm
V = π.r2.H
V = π. (3,1)2. 10
V = π. 9,61. 10
V = π. 96,1
V = 3.14. 96,1
V = 301.7 cm3
2. A cylindrical drum has a base of 60 cm in diameter and a height of 100 cm. Calculate the capacity of this drum. Use the value of 3.14 for π.
First, let's find the radius of this figure by dividing the diameter value by 2:
60: 2 = 30 cm
So, just put the values in the formula:
V = π.r2.H
V = π. (30)2. 100
V = π. 900. 100
V = 90,000 π
V = 282,600 cm3
Entrance Exam Exercises with Feedback
The theme of cylinder volume is much explored in the entrance exams. So, check below two exercises that fell in ENEM:
1. The figure below shows a water reservoir in the form of a straight circular cylinder, 6 m high. When it is completely full, the reservoir is enough to supply, for a day, 900 homes whose average daily consumption is 500 liters of water. Suppose that, one day, after a water use awareness campaign, the residents of the 900 houses supplied by this reservoir saved 10% in water consumption. In this situation:

a) the amount of water saved was 4.5 m3.
b) the height of the water level left in the reservoir, at the end of the day, was equal to 60 cm.
c) the amount of water saved would be sufficient to supply a maximum of 90 homes whose daily consumption was 450 liters.
d) the residents of these houses would save more than R$ 200.00 if the cost of 1 m3 of water for the consumer was equal to R$ 2.50.
e) a reservoir of the same shape and height, but with a base radius 10% smaller than that shown, would have enough water to supply all the houses.
Answer: letter b
2. (Enem/99) A cylindrical bottle is closed, containing a liquid that almost completely occupies its body, as shown in the figure. Suppose that, to take measurements, you only have a millimeter ruler.

To calculate the volume of liquid contained in the bottle, the minimum number of measurements to be performed is:
to 1
b) 2
c) 3
d) 4
e) 5
Answer: letter b
practice with 13 exercises on cylinders.