Trapezium Area: Calculation of Trapezium Area

THE trapeze area measures the surface value of this flat figure formed by four sides.

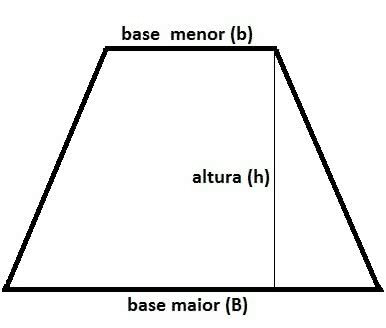
The trapeze is a quadrilateral that has two sides and two parallel bases, one larger and one smaller.

The trapeze is considered a remarkable quadrilateral, so the sum of its internal angles corresponds to 360°.

Trapeze Classification

Trapezies are classified into three types:

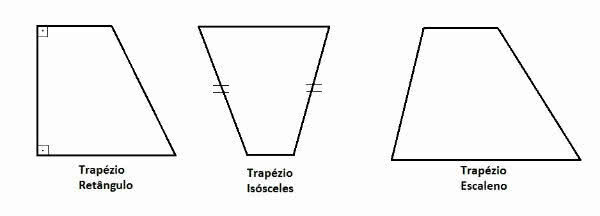
• Rectangle Trapeze: presents two 90º angles, called right angles.
• Isosceles or Symmetrical Trapezium: non-parallel sides are congruent (have the same measurement).
• Scalene Trapeze: all sides have different measurements.

Area formula

To calculate the trapeze area we use the following formula:

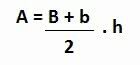
Where:

THE: figure area
B: larger base
B: smaller base
H: height

Perimeter formula

To calculate the perimeter of the trapeze, the formula is used:

P = B + b + L₁ + L₂

Where:

P: perimeter (sum of all sides)
B: larger base
B: smaller base
L₁ and L_2: sides of the figure

Learn more about the topic in the articles:

• trapeze
• plane geometry
• Area and Perimeter
• Polygon Area
• Perimeters of Flat Figures
• Flat Figure Areas
• Flat Figures Area - Exercises

Solved Exercises

1. Calculate the area of ​​a trapeze with a height of 5 cm and bases of 8 cm and 3 cm.

See Answer

B: 8cm
b: 3 cm
h: 5 cm

To calculate your area, just replace the values ​​in the formula:

A = 8+3/2. 5
A = 11/2. 5
A = 5.5. 5
H = 27.5 cm²

2. Determine the measurement of the smallest base of a 100 cm trapezoid² of area, 10 cm in height and base greater than 15 cm.

See Answer

H: 100 cm²
h: 10 cm
B: 15 cm

By substituting the values ​​in the formula, we can find the lowest base value:

100 = 15 + b/2. 10
100 = 15 + b. 5
100/5 = 15 + b
20 -15 = b
b = 5 cm

To check if the value found is correct, substitute in the formula:

A = 15 + 5/2 .10
A = 20/2. 10
A = 20.5
H = 100 cm²

3. How tall is a trapeze with an area of ​​50 cm², base larger than 6 cm and smaller than 4 cm?

See Answer

H = 50 cm²
B = 6 cm
b = 4 cm

50 = 6 + 4/2. H
50 = 10/2. H
50 = 5h
h = 50/5
h = 10 cm

Once the value is found, check if it is correct, using the formula again:

A = 6 + 4/2. 10
A = 10/2. 10
A = 5. 10
H = 50 cm²

How about finding out more about the areas of other flat figures?

• Circle Area
• Triangle Area
• Diamond Area
• Square Area
• Rectangle Area
• Parallelogram Area
• Math Formulas