THE rectangle area corresponds to the product (multiplication) of the measure of the base by the height of the figure, being expressed by the formula:
A = b x h
Where,
THE: area
B: base
H: height
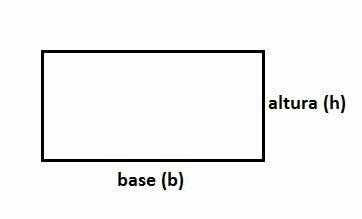
remember that the rectangle is a flat geometric figure formed by four sides (quadrilateral). Two sides of the rectangle are smaller and two of them are larger.
It has four internal 90° angles called right angles. Thus, the sum of the inner angles of the rectangles totals 360°.
How to calculate rectangle area?
To calculate the surface or area of the rectangle, just multiply the base value with the height.
To illustrate, let's see an example below:
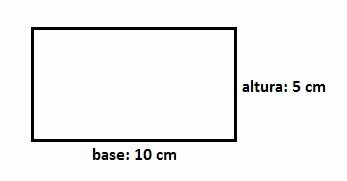
Applying the formula to calculate the area, in a rectangle of base 10 cm and height of 5 cm, we have:
Therefore, the figure area value is 50 cm2.
Rectangle Perimeter
Do not confuse the area with the perimeter,which corresponds to the sum of all sides. In the example above, the perimeter of the rectangle would be 30 cm. That is: 10 + 10 + 5 + 5 = 30.

The formula for calculating the perimeter is:
P = 2 x (b + h)
Where,
P: perimeter
B: base
H: height
Applying the formula to calculate the perimeter of the rectangle, base 10 cm and height 5 cm, we have:
Thus, in a rectangle whose base measures 10 cm and the height is 5 cm, the perimeter is 30 cm.
See also the articles:
- Rectangle Perimeter
- Area and Perimeter
- Perimeters of Flat Figures
Rectangle Diagonal
The line joining two non-consecutive vertices of a rectangle is called a diagonal. So, if we draw a diagonal on a rectangle, we see that two right triangles.
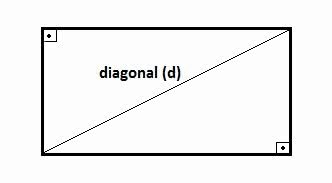
Thus, the calculation of the rectangle's diagonal is done through the Pythagorean theorem, where the value of the square of the hypotenuse is equal to the sum of the squares of its legs.
Therefore, the formula for calculating the diagonal is expressed as follows:
d2 = b2 + h2 or d =
Where,
d: diagonal
B: base
H: height
Applying the formula to calculate the diagonal, in a rectangle with a base of 10 cm and a height of 5 cm, we have:
Therefore, in a rectangle whose base measures 10 cm and the height is 5 cm, the diagonal of the figure is .
Attention!
You must observe the units of measurement given by the exercise, as the base and height must have the same units.
For example, if the unit is given in centimeters, the area will be in square centimeters (cm2), which corresponds to the multiplication between the measurement units (cm x cm = cm2).
Likewise, if it is given in meters, the area will be square meters (m2).
To broaden your search see also: plane geometry
Solved Exercises
To better fix the knowledge, check below two solved exercises on the rectangle area:
question 1
Calculate the area of a rectangle with a base of 8 m and a height of 2 m.

Correct answer: 16 m2.
In this exercise, just apply the area formula:
For more questions, see also: Flat Figures Area - Exercises.
question 2
Calculate the area of a rectangle that has a base of 3 m and a diagonal of m:
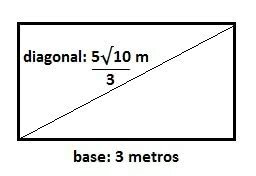
Correct answer: A = 13 m2.
To solve this problem, we first have to find the height value of the rectangle. It can be found by the diagonal formula:
After finding the height value, we used the area formula:
Therefore, the area of a rectangle is 13 square meters.
question 3
Look at the rectangle below and write the polynomial that represents the area of the figure. Next, calculate the area value when x = 4.
Correct answer: A = 2x2 - x - 3 and A(x = 4) = 25.
First, we replace the image data in the rectangle area formula.
To find the polynomial that represents the area we must multiply term by term. In the multiplication of equal letters, the letter is repeated and the exponents are added.
Therefore, the polynomial that represents the area is 2x2 - x - 3.
Now we replace the value of x with 4 and calculate the area.
So when we have x = 4, the area is 25 units.
Check out the other figures area:
- Flat Figure Areas
- Polygon Area
- Triangle Area
- Diamond Area
- Circle Area
- Square Area
- Trapeze Area
- Parallelogram Area