The condition of existence of a triangle is an obligatory characteristic in the lengths of its three sides. It ensures that the figure can be closed, that is, that the sides are connected by vertices.
A triangle is a figure formed by three straight, plane and, above all, closed segments. However, not every trio of segments manages to close the triangle.
For three segments to close a triangle, each side must be less than the sum of the other two.
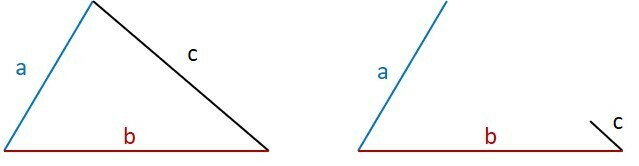
Any three sides, which we will call a, b and c, to be able to form a triangle, the measures must obey:
The three conditions must be satisfied. If one fails, it is not possible to close and form the triangle.
Example 1
Check that three segments measuring 4 cm, 7 cm and 12 cm can form a triangle.
- 4 < 7 + 12 (true)
- 7 < 4 + 12 (true)
- 12 < 4 + 7 (false), because 4 + 7 = 11 and 12 is not less than 11.
Therefore, it is not possible to form a triangle with the segments 4 cm, 7 cm and 12 cm.
Example 2
Check if it is possible to form a triangle with segments of 5 cm, 9 cm and 10 cm.
- 5 < 9 + 10 (true)
- 9 < 5 + 10 (true)
- 10 < 5 + 9 (true)
In this way, it is possible to form a triangle with the segments 5 cm, 9 cm and 10 cm.
Learn more about triangles at:
- Triangle: all about this polygon
- Classification of Triangles
- Exercises on triangles explained
- Triangle area: how to calculate?
Disable VerificationPremium Suggestions
ASTH, Rafael. Condition for the existence of a triangle (with examples).All Matter, [n.d.]. Available in: https://www.todamateria.com.br/condicao-de-existencia-de-um-triangulo/. Access at:
See too
- Exercises on triangles explained
- Classification of Triangles
- Triangle: all about this polygon
- 23 math exercises 7th grade
- Sum of interior angles of a polygon
- Exercises on answered angles
- Exercises on polygons
- Notable points of a triangle: what they are and how to find them