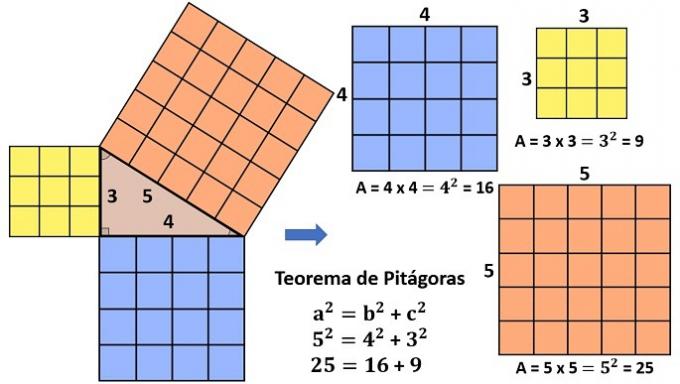
You perimeters of flat figures indicate the value of the outline measure of the figure. That is, the concept of perimeter corresponds to the sum of all sides of a flat geometric figure.
Let's see below the main figures that are part of Plane Geometry.
Main Flat Figures
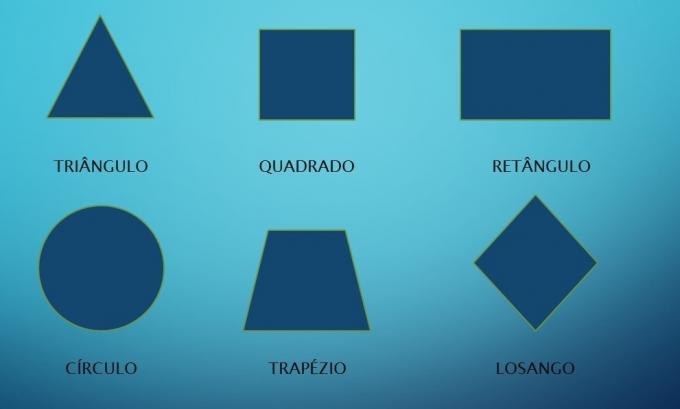
triangle
Flat figure formed by three sides and internal angles. According to the size of the sides they can be:
- Equilateral triangle: equal sides and internal angles (60°);
- isosceles triangle: two sides and two congruent internal angles;
- Scalene Triangle: all sides and inside angles are different.
And, according to the measurement of the angles, they are classified into:
- Rectangle Triangle: an internal angle of 90°;
- Obtuse Triangle: two internal acute angles (less than 90°), and an internal obtuse angle (greater than 90°);
- Acute Triangle: Three internal angles less than 90°.
Read more:
- Triangle Area
- Triangle Perimeter
- Triangle Classification
Square
Flat figure formed by four congruent sides (same measure). It has four internal 90° angles (right angles).
Read more:
- Square Area
- Square Perimeter
Rectangle
Flat figure formed by four sides, two of which are smaller. It also has four internal 90° angles.
Read more:
- Rectangle
- Rectangle Area
- Rectangle Perimeter
Circle
Flat figure that is also called a disk. It is formed by the radius (distance between the center and the edge of the figure) and the diameter (a segment of straight line that passes through the center and goes from one side to the other of the figure.
Read more:
- Circle Area
- Circle Perimeter
trapeze
Flat figure formed by four sides. It has two sides and parallel bases, one smaller and one larger. According to the measurement of the sides and angles they are classified into:
- Rectangle Trapeze: has two 90º angles;
- Isosceles or Symmetrical Trapezium: non-parallel sides have the same measurement;
- Scalene Trapeze: all sides have different measurements.
Read more:
- trapeze
- Trapeze Area
Diamond
Flat figure formed by four equal sides. It has congruent and parallel opposite sides and angles.
Know about the Diamond Area.
Perimeter and Area of Flat Figures
There is often confusion between the concept of area and perimeter. However, area is the measure of the surface of a flat figure. The perimeter is the sum of the measurements on the sides of the figure.
Learn more about the topic:
- Area and Perimeter
- Flat Figure Areas
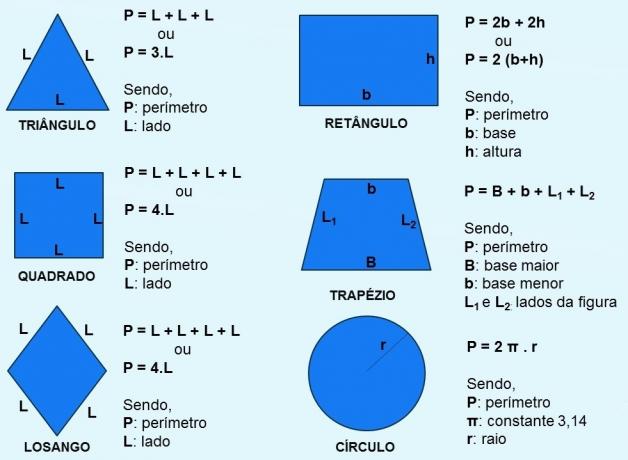
Perimeter Formulas
To calculate each of the flat figures presented above, the following formulas are used:
Also read about Quadrilaterals.
Exercise solved
Check below an exercise that fell on Enem and involves both the concept of perimeter and area:
(Enem-2011) In a certain city, residents of a neighborhood lacking leisure spaces demand the construction of a square from the city hall. The city hall agrees with the request and states that it will build it in a rectangular shape due to the technical characteristics of the land. Budgetary restrictions impose that a maximum of 180 m of canvas be used to surround the square. The city hall presents to the residents of this neighborhood the measurements of the land available for the construction of the square:
Land 1: 55 m by 45 m
Land 2: 55 m by 55 m
Plot 3: 60 m by 30 m
Land 4: 70 m by 20 m
Land 5: 95 m by 85 m
To opt for the land with the largest area, which meets the restrictions imposed by the city hall, residents must choose the land.
to 1
b) 2
c) 3
d) 4
e) 5
To answer this question, we must first calculate the perimeter of each terrain, to analyze whether it meets the restrictions. And then calculate the area of the rectangular region.
We know that to find the perimeter of the rectangle, the formula is used:
2(b + h)
Thus,
Land 1: 2. (55 + 45) = 200
Land 2: 2. (55 + 55) = 220
Land 3: 2. (60 + 30) = 180
Land 4: 2. (70 + 20) = 180
Land 5: 2. (95 + 85) = 360
According to the restriction, two of them fit the proposal. Therefore, we must calculate the area of land 3 and 4:
Land 3:
A=b.h
A = 60. 30
A = 1800 m2
Land 4:
A=b.h
A = 70. 20
A = 1400 m2
Therefore, we came to the conclusion that land 3, in addition to meeting the restriction, has the largest area.
Alternative C
Check out more questions, with commented resolution, in Area and Perimeter Exercises.