Practice exercises on triangles with this list that we have prepared. The exercises are explained step by step so you can clear your doubts and learn everything about this three-sided polygon.
question 1
Analyze the following figure formed by triangles and determine the measure of the segment ED, parallel to AB, knowing that:
CD = 15
AD = 1
AB = 8

Since DE is parallel to AB, triangles CDE and CAB are similar. We can thus write the ratios between their corresponding sides
AC = AD + DC = 1 + 15 = 16.
question 2
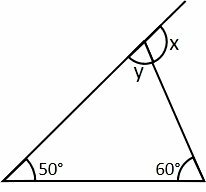
In the image below, determine the value of angle x in degrees.
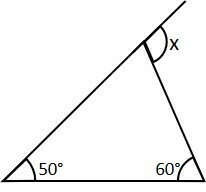
Answer: 110 degrees
According to the exterior angle theorem, an angle exterior to a vertex is equal to the sum of the interior angles of the two others.
x = 50 degrees + 60 degrees = 110 degrees
Another way to solve the question is to add the three interior angles and make them equal to 180º. Thus, calling the supplementary interior angle to x y, its value is
 :
:
50 + 60 + y = 180
110 + y = 180
y = 180 - 110
y = 70º
If y is equal to 70 degrees, x is how far it takes to get to 180.
x = 180 degrees - 70 degrees = 110 degrees
question 3
Determine the length of segment x.

Answer: 2.4m
The figure is formed by two similar triangles. The two have right angles and equal angles opposite by the common vertex between them. By the case of AA (angle-angle) similarity, we confirm the similarity.
Taking the ratio of their corresponding sides, we have:
question 4
The figure below shows a rectangle with a base of 8 cm and a height of 1 cm, inscribed in a triangle. The base of the rectangle is coincident with the base of the triangle. Determine the measure of height h.

Answer: h = 2 cm
We can determine two similar triangles: one with base 12 cm and height x cm and the other with base 8 cm (base of the rectangle) and height h.
Proportioning the corresponding sides, we have:
See that x is equal to the height h plus the height of the rectangle.
x = h + 1
Replacing:
question 5
Fernando is a carpenter and is separating wooden slats of different lengths to build triangular structures.
Among the following options of slat trios, the only one capable of forming a triangle is
a) 3 cm, 7 cm, 11 cm
b) 6 cm, 4 cm, 12 cm
c) 3 cm, 4 cm, 5 cm
d) 7 cm, 9 cm, 18 cm
e) 2 cm, 6 cm, 9 cm
The condition for the existence of a triangle says that each of its sides must be less than the sum of the other two.
The only option that satisfies this condition is the letter c.
question 6
In the triangle below, the lines and segments: green, red, blue and black are: respectively:
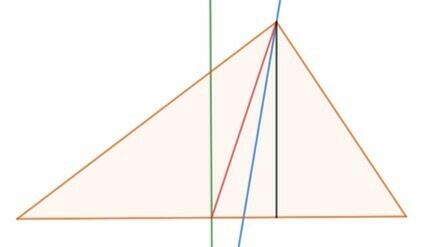
Response:
Green: bisector. It is the line that cuts a segment at its midpoint at a 90° angle.
Red: medium. It is the segment that runs from a vertex to the midpoint of the opposite side.
Blue: bisector. Divides an angle into two congruent angles.
Black: height. It is the segment that leaves a vertex and goes to the opposite side, making a 90º angle.
question 7
(ENCCEJA 2012)A patchwork quilt, with a rectangular shape, is made with four triangular pieces of fabric, as shown in the figure.

Consider that the seams along the diagonals of this quilt are perfectly straight.
Piece A of the quilt, which has the shape of a triangle, can be classified according to its internal angles and sides, respectively, as
a) acute and equilateral.
b) obtuse and scalene.
c) obtuse and isosceles.
d) rectangle and isosceles.
Flap A is obtuse because it has an obtuse angle greater than 90º.
Since the quilt is a rectangle and the separations of the triangles are formed by two diagonals, the internal sides are equal, two by two.
As the flap has two equal sides, it is isosceles.
question 8
In the triangle ABC shown in the figure below, AD is the bisector of the interior angle at A and . The interior angle at A is equal to

a) 60º
b) 70º
c) 80º
d) 90º
Segment AD is a bisector and divides angle A into two equal angles. Since the triangle ADB has two equal sides, AD and BD, it is isosceles, and the base angles are equal.
Thus, we have the 60º angle and three others equal.
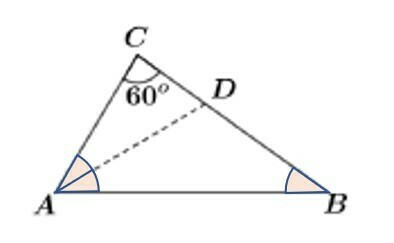
Calling x the unknown angle, we have:
60 + x + x + x = 180
60 + 3x = 180
3x = 180 - 60
3x = 120
x = 120/3
x = 40
If x = 40 and the angle at A is formed by 2x, then:
A = 2x
A = 2.40 = 80 degrees
question 9
(Enem 2011) To determine the distance from a boat to the beach, a navigator used the following procedure: from point A, he measured the visual angle by aiming at a fixed point P on the beach. Keeping the boat in the same direction, he proceeded to a point B so that it was possible to see the same point P from the beach, however, under a visual angle 2α. The figure illustrates this situation:

Suppose the navigator had measured the angle α = 30º and, upon reaching point B, verified that the boat had traveled the distance AB = 2000 m. Based on these data and maintaining the same trajectory, the shortest distance from the boat to the fixed point P will be
a) 1000 m.
b) 1 000√3 m.
c) 2 000√3/3 m.
d) 2000 m.
e) 2 000√3 m
Resolution
Data
= 30º
= 2000 meters
Step 1: supplement 2.
if the angle is 30 degrees, 2
= 60º and its supplementary, what is missing for 180º, is 120º.
180 - 60 = 120
Step 2: Determine the interior angles of the triangle ABP.
Since the sum of the interior angles of a triangle is 180°, the angle must be 30º, because:
30 + 120 + P = 180
P = 180 - 120 - 30
P = 30
Thus, the triangle ABP is isosceles and the sides AB and BP have the same length.
Step 3: Determine the shortest distance between the boat and point P.
The smallest distance is the perpendicular segment between point P and the dotted line, which represents the path of the boat.
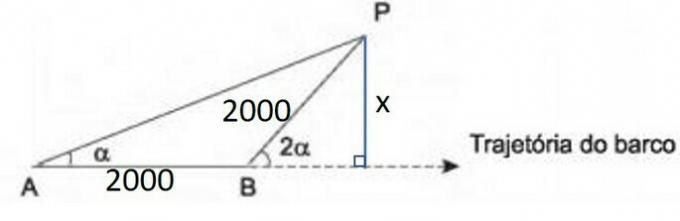
Segment BP is the hypotenuse of the right triangle.
The sine of 60° relates the distance x and the hypotenuse BP.
Conclusion
The shortest distance between the boat and point P on the beach is 1000 m.
question 10
(UERJ - 2018)
I gather this sunlight around me,
In my prism I disperse and recompose:
Rumor of seven colors, white silence.
JOSÉ SARAMAGO
In the following image, triangle ABC represents a plane section parallel to the base of a straight prism. The lines n and n' are perpendicular to the sides AC and AB, respectively, and BÂC = 80°.
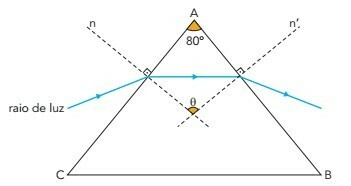
The measure of the angle θ between n and n' is:
a) 90º
b) 100 degrees
c) 110º
d) 120º
In the triangle with vertex A of 80º and base formed by the ray of light, parallel to the larger base, we can determine the internal angles.
As the prism is straight and the light base of the triangle with apex at A is parallel to the larger base, these angles are equal. Since the sum of the interior angles of a triangle equals 180°, we have:
80 + x + x = 180
2x = 180 - 80
2x = 100
x = 100/2
x = 50
Adding the 90º angle formed by the dotted lines, we have 140º.
Thus, the interior angles of the smaller triangle facing downwards are:
180–140 = 40
Using the sum of the interior angles again, we have:
40 + 40 + = 180
= 180 - 80
= 100º
Continue your studies on triangles:
- Triangle: all about this polygon
- Classification of triangles
- Triangle area: how to calculate?
- Trigonometry in the right triangle
ASTH, Rafael. Exercises on triangles explained.All Matter, [n.d.]. Available in: https://www.todamateria.com.br/exercicios-sobre-triangulos-explicados/. Access at:
See too
- Classification of Triangles
- Triangle: all about this polygon
- Triangle Area
- Exercises on quadrilaterals with explained answers
- Exercises on answered angles
- Similarity of triangles: commented and solved exercises
- Notable points of a triangle: what they are and how to find them
- Condition for the existence of a triangle (with examples)