THE triangle area can be calculated from the measurements of the base and height of the figure. Remember that a triangle is a flat geometric figure formed by three sides.
However, there are several ways to calculate the area of a triangle, the choice being made according to the known data in the problem.
It turns out that many times, we don't have all the necessary measurements to make this calculation.
In these cases, we must identify the type of triangle (rectangle, equilateral, isosceles or scalene) and take into account their characteristics and properties to find the measurements that we need.
How to calculate the area of a triangle?
In most situations, we use the measurements of the base and height of a triangle to calculate its area. Consider the triangle shown below, its area will be calculated using the following formula:
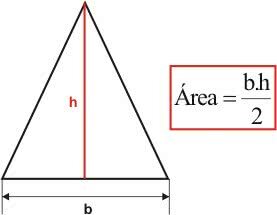
Being,
Area: triangle area
B: base
H:height
Rectangle Triangle Area
O right triangle it has a right angle (90º), and two acute angles (smaller than 90º). In this way, of the three heights of a right triangle, two coincide with the sides of that triangle.
Also, if we know two sides of a right triangle, using the Pythagorean theorem, we easily found the third side.

Equilateral Triangle Area
O equilateral triangle, also called an equiangle, is a type of triangle that has all sides and congruent interior angles (same measurement).
In this type of triangle, when we only know the side measure, we can use Pythagoras' theorem to find the height measure.
Height in this case divides it into two other congruent triangles. Considering one of these triangles and that its sides are L, h (height) and L/2 (the side related to height is divided in half), we are left with:
Thus, substituting the value found for the height in the area formula, we have:
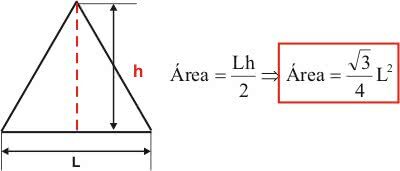
Isosceles Triangle Area
O isosceles triangle is a type of triangle that has two congruent sides and two congruent interior angles. To calculate the area of the isosceles triangle, use the basic formula for any triangle.
When we want to calculate the area of an isosceles triangle and we don't know the height measure, we can also use Pythagoras' theorem to find that measure.
In the isosceles triangle, the height relative to the base (side measuring different from the other two sides) divides this side into two congruent segments (same measure).
In this way, knowing the measurements of the sides of an isosceles triangle, we can find its area.
Example
Calculate the area of the isosceles triangle represented in the figure below:

Solution
To calculate the area of the triangle using the basic formula, we need to know the height measure. Considering the base as the side of different measurement, we will calculate the height relative to that side.
Remembering that the height, in this case, divides the side into two equal parts, we will use the Pythagorean theorem to calculate its measure.
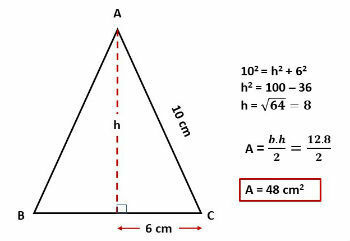
Scalene Triangle Area
O scalene triangle is a type of triangle that has all different sides and inside angles. Therefore, one way to find the area of this type of triangle is to use the trigonometry.
If we know two sides of this triangle and the angle between these two sides, its area will be given by:


By Heron's Formula we can also calculate the area of the scalene triangle.
Other formulas for calculating triangle area
In addition to finding the area through the product of the base by the height and dividing by 2, we can also use other processes.
Heron's formula
Another way to calculate the area of the triangle is by "Heron's formula", also called "Hero's Theorem". It uses the semiperimeters (half the perimeter) and sides of the triangle.
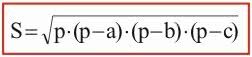
Where,
s: triangle area
P: semiperimeter
The, B and ç: sides of the triangle
The perimeter of the triangle being the sum of all sides of the figure, the semiperimeter represents half of the perimeter:
It is interesting to note that, in this formula, there is no need to know the height measurement (h), therefore, when this information is not given, the "Heron's Theorem" makes it easier to find the area of triangle.
Circumscribed Radius Formula
Based on "law of sins" you have to "Circumscribed Radius Formula" represented by the expression:
THE: triangle area
The, B and ç: sides of the triangle
r: radius of circumscribed circumference
It is used when the triangle is inscribed on a circle.
Entrance Exam Exercises with Feedback
1. Enem - 2010
On construction sites, it is common to see workers measuring lengths and angles and demarcating where the work should start or rise.
In one of these beds some marks were made on the flat floor. It was possible to notice that, of the six piles placed, three were vertices of a right triangle and the other three were the midpoints of the sides of this triangle as seen in the figure, where the stakes have been indicated by letters.
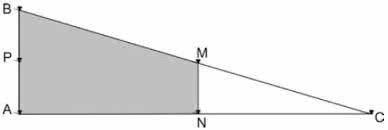
The region demarcated by stakes A, B, M and N should be paved with concrete. Under these conditions, the area to be paved corresponds
a) to the same area as the AMC triangle.
b) to the same area as the triangle BNC.
c) half of the area formed by triangle ABC.
d) twice the area of the MNC triangle.
e) to triple the area of the triangle MNC.
Alternative e: to triple the area of the triangle MNC.
2. Cefet/RJ - 2014
If ABC is a triangle such that AB = 3 cm and BC = 4 cm, we can say that its area, in cm2, is a number:
a) at most equal to 9
b) at most equal to 8
c) at most equal to 7
d) at most equal to 6
Alternative d: maximum equal to 6
3. PUC/RIO - 2007
The hypotenuse of a right triangle measures 10 cm and the perimeter measures 22 cm. The area of the triangle (in cm2) é:
a) 50
b) 4
c) 11
d) 15
e) 7
Alternative c: 11
To learn more, read also:
- Polygon Area
- Square Area
- Flat Figure Areas
- Flat Figures Area - Exercises
- Rectangle Area
- Area and Perimeter
- Pythagoras Theorem - Exercises
- plane geometry
- Rectangle
- Prism
- Math Formulas