We know that a complex number has a geometric form equal to z = a + bi, where a is called the real part and b the imaginary part of z. For example, for the complex number z = 3 + 5i, we have a = 3 and b = 5 or Re (z) = 3 and Im (z) = 5. Complex numbers also have a trigonometric or polar form, which will be demonstrated based on the argument of z (for z ≠ 0).
Consider the complex number z = a + bi, where z ≠ 0, so we have: cosӨ = w/w and sinӨ = b/p. These relationships can be written in another way, follow:
cosӨ = a/p → a = p*cosӨ
sinӨ = b/p → b = p*sinӨ
Let's substitute the values of a and b into the z = a + bi complex.
z = p*cosӨ + p*senӨi → z = p*( cosӨ + i*senӨ)
This trigonometric form is very useful in calculations involving potentiations and radiciations.
Example 1
Represent the complex number z = 1 + i in trigonometric form.
Resolution:
We have that a = 1 and b = 1 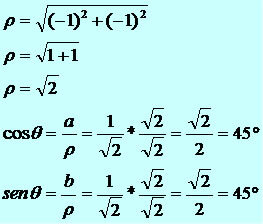
The trigonometric form of the complex z = 1 + i is z = √2*(cos45th + sin45th * i).
Example 2
Trigonometrically represent the complex z = –√3 + i.
Resolution:
a = –√3 and b = 1
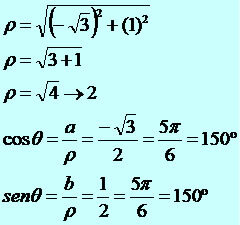
The trigonometric form of the complex z = –√3 + i is z = 2*(cos150th + sin150th * i).
Do not stop now... There's more after the advertising ;)
by Mark Noah
Graduated in Mathematics
Brazil School Team
Complex numbers - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Trigonometric Shape of a Complex Number"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/forma-trigonometrica-um-numero-complexo.htm. Accessed on June 29, 2021.