Taxi geometry or Pombaline geometry is one of several non-Euclidean geometries. Euclidean geometry can describe countless real situations. However, she cannot answer some questions. For example: What is the shortest distance between your home and work? In Euclidean view, the shortest distance between two points is a straight line. But, most likely, the distance between home and work does not describe a straight trajectory.
In taxi geometry, the shortest distance between two points on a plane is not the straight line. Distance is not measured like the flight of a bird, but like the journey of a taxi in a city whose streets stretch out. vertically and horizontally in a block or urban mesh, which can conveniently be associated with the plan Euclidean.
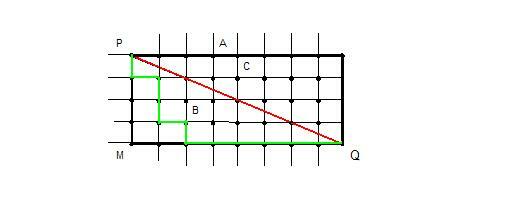
Let's consider that we want to leave point P towards point Q, covering the shortest distance. In this situation, the horizontal and vertical lines are streets and each quadrilateral formed in the mesh represents a block or block.
See the picture:

For Euclidean geometry, the shortest distance between points P and Q is the red line represented in the figure. In reality this would be impossible, as the taxi would have to pass within the blocks. In the taxi geometry, the shortest distance would be given by the paths described by the segments in blue and orange.
See the interesting thing about this geometry: Consider that each side of the block has a unit measure, that is, each side measures 1. Thus, the distance between points P and Q, according to the blue path, is 12. The second orange path is also 12. Now, let's assume that the taxi takes the path described in green in the figure below:
Do not stop now... There's more after the advertising ;)
Remembering that each side of the block measures 1, the distance between P and Q, in this case, is also 12.
In general, the distance between two points P(x1, y1) and Q(x2, y2) on the plane in the taxi geometry is given by:
DPQ = |X1 – X2| + |Y1 – Y2|
By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
plane geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
RIGONATTO, Marcelo. "Taxi geometry"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/geometria-taxi.htm. Accessed on June 28, 2021.