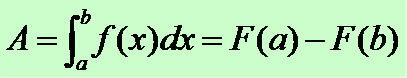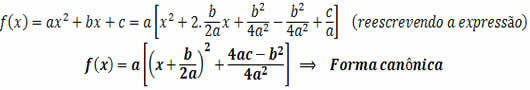A 1st degree inequality system is formed by two or more inequalities, each of which has only one variable, which must be the same in all other inequalities involved.
When we finish solving a system of inequalities we arrive at a solution set, this is composed of possible values that x must assume for the system to exist.
To arrive at this solution set, we must find the solution set of each inequality involved in the system, from there we make the intersection of these solutions.
The set formed by the intersection we call SOLUTION SET of the system.
See some examples of 1st degree inequality system: 
Let's find the solution for each inequality.
4x + 4 ≤ 0
4x ≤ - 4
x ≤ - 4: 4
x ≤ - 1 
S1 = {x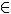 
R | x ≤ - 1}
Calculating the second inequality we have:
x + 1 ≤ 0
x ≤ - 1
The “ball” is closed, as the sign of inequality is equal.
S2 = {x 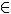R | x ≤ - 1}
Calculating now the SOLUTION SET of the inequality we have:
S = S1 ∩ S2 
Therefore:
S = { x 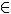R | x ≤ - 1} or S = ] - ∞; -1]
First, we must calculate the solution set of each inequality.
3x + 1 > 0
3x > -1
x > -1
3
The “ball” is open, as the sign of inequality is not equal.
We now calculate the solution set of the other solution.
5x - 4 ≤ 0
5x ≤ 4
x ≤ 4
5
Now we can calculate the SOLUTION SET of the inequality, so we have:
S = S1 ∩ S2
Therefore:
S = { x R | -1 < x ≤ 4} or S = ] -1; 4]
3 5 3 5
We must organize the system before solving it, see how it looks:
Calculating the solution set of each inequality we have:
10x - 2 ≥ 4
10x ≥ 4 + 2
10x ≥ 6
x ≥ 6
10
x ≥ 3
5
6x + 8 < 2x + 10
6x -2x < 10 - 8
4x < 2
x < 2
4
x < 1
2
We can calculate the SOLUTION SET of the inequality, so we have:
S = S1 ∩ S2
Observing the solution, we will see that there is no intersection, so the solution set of this inequality system will be:
S =
Do not stop now... There's more after the advertising ;)
by Danielle de Miranda
Graduated in Mathematics
Brazil School Team
Roles - 1st Degree Function - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
RAMOS, Danielle de Miranda. "1st degree inequality system"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/sistema-inequacao-1-grau.htm. Accessed on June 28, 2021.
