Every function defined by the formation law f (x) = logThex, with a ≠ 1 and a > 0 is called the base logarithmic function. The. In this type of function, the domain is represented by the set of real numbers greater than zero and the counterdomain, the set of reals.
Examples of logarithmic functions:
f(x) = log2x
f(x) = log3x
f(x) = log1/2x
f(x) = log10x
f(x) = log1/3x
f(x) = log4x
f(x) = log2(x - 1)
f(x) = log0,5x
Determining the domain of the logarithmic function
Given the function f(x) = log(x – 2) (4 - x), we have the following restrictions:
1) 4 – x > 0 → – x > – 4 → x < 4
2) x – 2 > 0 → x > 2
3) x – 2 ≠ 1 → x ≠ 1+2 → x ≠ 3
Performing the intersection of restrictions 1, 2 and 3, we have the following result: 2 < x < 3 and 3 < x < 4.
Thus, D = {x? R / 2 < x < 3 and 3 < x < 4}
Graph of a logarithmic function
For the construction of the logarithmic function graph, we must be aware of two situations:
? to > 1
? 0 < to < 1
For > 1, we have the graph as follows:
increasing function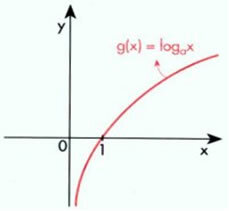
Do not stop now... There's more after the advertising ;)
For 0 < a < 1, we have the graph as follows:
Descending function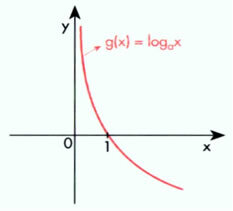
Characteristics of the logarithmic function graph y = logThex
The graph is all the way to the right of the y axis as it is set to x > 0.
Intersects the abscissa axis at point (1.0), so the root of the function is x = 1.
Note that y assumes all real solutions, so we say that Im (picture) = R.
Through the studies of logarithmic functions, we came to the conclusion that it is an inverse function of the exponential. Look at the comparative chart below:
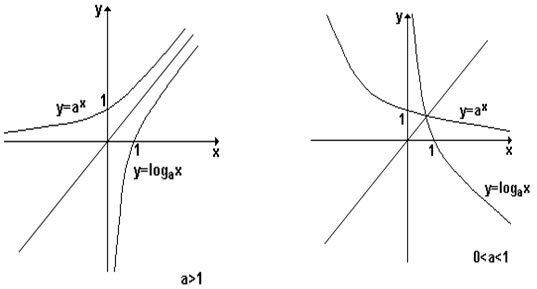
We can note that (x, y) is in the graph of the logarithmic function if its inverse (y, x) is in the exponential function of the same base.
by Mark Noah
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Logarithmic Function"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/funcao-logaritmica.htm. Accessed on June 29, 2021.