Functions have some properties that characterize them f: A→B.
Overjet function
Injector function
Bijector function
inverse function
Overjet function: a function is surjective if and only if its image set is specifically equal to the counterdomain, Im = B. For example, if we have a function f: Z→Z defined by y = x +1 it is surjective, since Im = Z.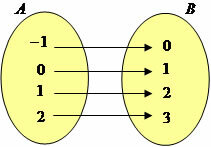
Injector function: a function is injective if the distinct elements of the domain have distinct images. For example, given the function f: A→B, such that f(x) = 3x.
Bijector function: a function is bijective if it is both injecting and surjective. For example, the function f: A→B, such that f (x) = 5x + 4.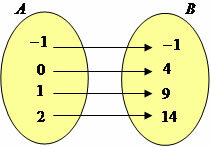
Do not stop now... There's more after the advertising ;)
Note that it is injecting, as x1≠x2 implies f (x1) ≠f (x2)
It is surjective, because for every element in B there is at least one in A, such that f(x)=y.
inverse function: a function will be inverse if it is bijector. If f: A→B is considered bijector then it admits inverse f: B→A. For example, the function y = 3x-5 has inverse y = (x+5)/3.
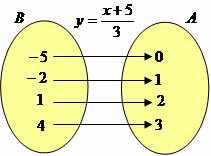
We can establish the following diagram: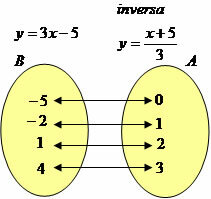
Note that the function has a relation of A→B and B→A, so we can say that it is inverse.
by Mark Noah
Graduated in Mathematics
See more!
1st degree function
Analyzing a linear function.
2nd degree function
Study of the Parable.
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Function Types"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/tipos-de-funcao.htm. Accessed on June 27, 2021.