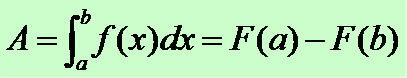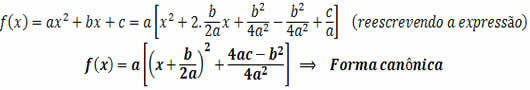Type functions y = ax + b or f (x) = ax + b, where a and b assume real values and a ≠ 0 are considered 1st degree functions. This function model has as its geometric representation the figure of a straight line, the position of this straight line being dependent on the value of the coefficient a. Watch:
Ascending function: a > 0. 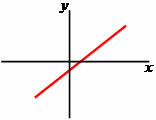
Descending function: a < 0.
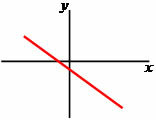
Function root
Calculating the value of the root of the function is to determine the value at which the line crosses the x axis, for that we consider the value of y equal to zero, because at the moment the line intersects the x axis, y = 0. Note the following graphic representation:

We can establish a general formation for the calculation of the root of a 1st degree function, just create a generalization based on the function formation law itself, considering y = 0 and isolating the value of x (root of occupation). Look:
y = ax + b
y = 0
ax + b = 0
ax = -b
x = -b/a
Therefore, to calculate the root of a 1st degree function, just use the expression x = x = –b/a.
Do not stop now... There's more after the advertising ;)
Example 1
Find the root of the function y = 2x – 9, this is when the line of the function intersects the x-axis.
Resolution:
x = -b/a
x = –(–9)/2
x = 9/2
x = 4.5
Example 2
Given the function f(x) = –6x + 12, determine the root of this function.
Resolution
x = -b/a
x = -12 / -6
x = 2
by Mark Noah
Graduated in Mathematics
Brazil School Team
1st degree function - Occupation - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Root of a 1st Degree Function"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/raiz-uma-funcao-1-grau.htm. Accessed on June 27, 2021.