One 1st degree function or affine function is defined by the training law f (x) = a.x + b, in which The and B are real and The ≠ 0. But among the wide range of functions 1st degree, there is a particular type of great importance: a linear function.
The linear function is the one where we have b = 0, that is, its formation law is of the type f(x) = a.x, with The real and different than zero. Note that every function that has no value for the coefficient B is classified as linear function and, consequently, it is also an affine function.
Let's look at some examples of linear function and their respective graphics:
Example 1: f (x) = 2x
This is a linear function that can be classified as growing, once a = 2 > 0. We can see your graphic in the image below:
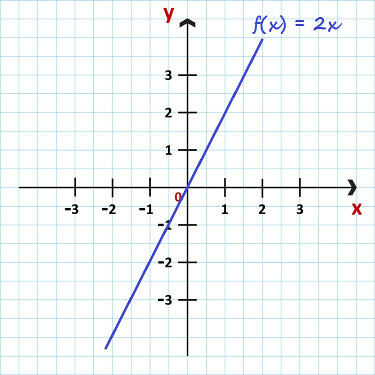
Graph of the function f (x) = 2x
Example 2: f(x) = – x
2
This is a decreasing linear function because a = – ½ < 0. Look at your graphic in the following figure:
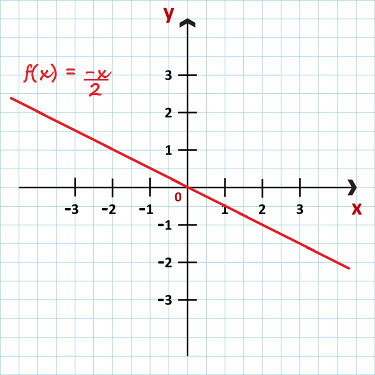
Graph of the function f (x) = – x/2
Do not stop now... There's more after the advertising ;)
Example 3: f (x) = 3x
This is a linear function classified as ascending since a = 3 > 0. We can see your graphic in the image below:
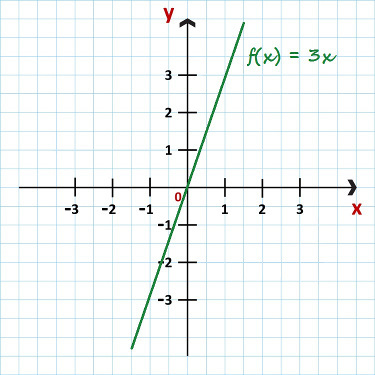
Graph of the function f (x) = 3x
Example 4: f (x) = – x
This is a linear decreasing function. It is classified as such because a = – 1 < 0. See your chart:

Graph of the function f (x) = – x
Note that in all of the previous examples the graphics have something in common. This is a very important feature of the linear function graph: the line always intersects the x and y axes at the origin of the coordinates (0,0).
Example 5: f(x) = x
Here we have an increasing linear function, because a = 1 > 0. But in addition to being a linear function f(x) = x, is also a identity function — which is of the type f(x) = a.x, with a = 1. See below what the identity function graph looks like:
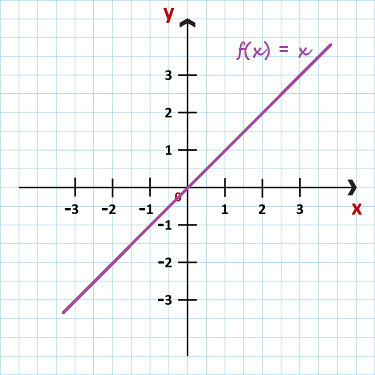
Identity function graph - f (x) = x
By Amanda Gonçalves
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
RIBEIRO, Amanda Gonçalves. "Linear Function"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/funcao-linear.htm. Accessed on June 27, 2021.