O stevin's theorem is the law that states that the pressure variation between two points of a fluid is determined by the product of fluid density, gravity acceleration and height variation between these points. Through Stevin's theorem it was possible to formulate Pascal's theorem and the principle of communicating vessels.
Read too: Buoyancy — the force that arises when a body is inserted into a fluid
Topics of this article
- 1 - Summary about Stevin's theorem
- 2 - What does Stevin's theorem say?
- 3 - Stevin's theorem formula
-
4 - Consequences and applications of Stevin's theorem
- → Principle of communicating vessels
- → Pascal's theorem
- 5 - Stevin's theorem measurement units
- 6 - Solved exercises on Stevin's theorem
Summary about Stevin's theorem
Stevin's theorem is the fundamental law of hydrostatic and was developed by scientist Simon Stevin.
According to Stevin's theorem, the closer a body is to sea level, the lower the pressure on it.
The main applications of Stevin's theorem are communicating vessels and Pascal's theorem.
In communicating vessels, the height of the liquids is the same regardless of the shape of the vessel, only changing if the placed liquids have different densities.
Pascal's theorem states that the pressure suffered in a point of a liquid will be transferred to the rest of it, considering that all suffered with the same pressure variation.
Do not stop now... There's more after the publicity ;)
What does Stevin's theorem say?
Also known as the fundamental law of hydrostatics, Stevin's theorem was formulated by the scientist Simon Stevin (1548-1620). It is stated as follows:
The pressure difference between the two points of a homogeneous liquid in equilibrium is constant, depending only on the difference in level between these points.1|
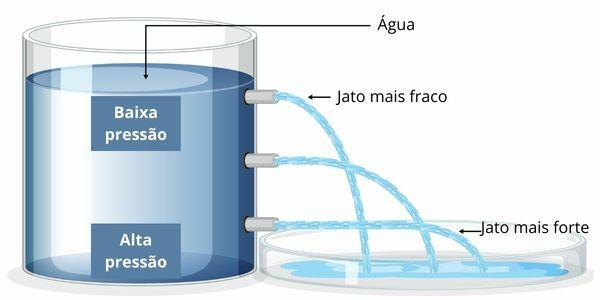
It deals with the variation of atmospheric pressure and hydraulic (in liquids) at different heights or depths. Like this, The more on the surface or at sea level a body is, the less pressure it experiences.. However, as this difference increases, the greater the pressure on the body, as we can see in the following image:
Stevin's Theorem Formula
\(∆p=d\cdot g\cdot∆h\) or \(p-p_o=d\cdot g\cdot∆h\)
\(∆p\) → gauge pressure or pressure variation, measured in Pascals \([Shovel]\).
P → absolute or total pressure, measured in Pascals \([Shovel]\).
\(dust\) → atmospheric pressure, measured in Pascals \([Shovel]\).
d → density or specific mass of the fluid, measured in\([kg/m^3]\).
g → gravity, measured in \([m/s^2]\).
\(∆h\) → height variation, measured in meters \([m]\).
Consequences and applications of Stevin's theorem
Stevin's theorem applied in different situations of daily life, such as the hydraulic system of the houses and the proper location for installing water tanks. In addition, its formulation enabled the development of the principle of communicating vessels and the Pascal's theorem.
→ Principle of communicating vessels
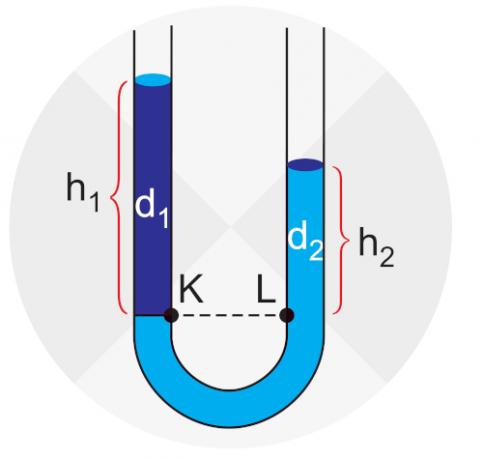
The principle of communicating vessels states that in a container composed of branches that are interconnected, when pouring a liquid of the same density on the branches, it will have the same level and will experience the same pressure in any of the parts. Next, we can see what the communicating vessels look like:

If liquids with different densities are placed in a U-shaped container, the heights of the liquids and the pressures exerted on them will be different, as we can see in the following image:
◦ Formula of the principle of communicating vessels
The principle of communicating vessels can be calculated using its formula:
\(\frac{H_1}{H_2} =\frac{d_2}{d_1} \) or H1∙d1=H2∙d2
\(H_1\) It is \(H_2\) → heights related to areas, measured in meters \([m]\).
\(d_1\) It is \(d_2\) → fluid densities, measured in\([kg/m^3]\).
This principle allows the toilets to contain the same level of water and it is possible to measure the pressure and density of fluids in laboratories.
→ Pascal's theorem
Formulated by scientist Blaise Pascal (1623-1662), the Pascal's theorem states that when pressure is applied to a point in a liquid in equilibrium, this variation will propagate to the rest of the liquid, causing all its points to suffer the same variation of pressure.
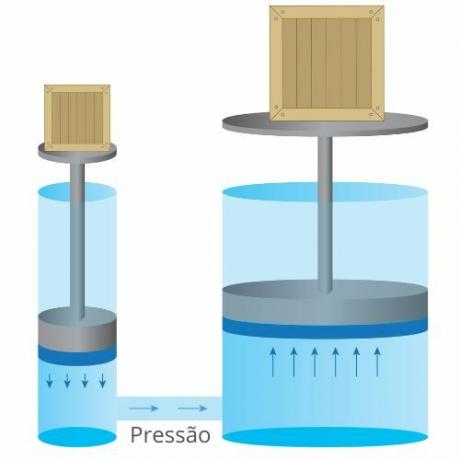
Through this theorem, the hydraulic press was developed. If we apply a strength downwards on one piston, there will be an increase in pressure that will cause the displacement of the fluid to the other piston, causing its elevation, as we can see in the following image:
◦ Pascal's theorem formula
Pascal's theorem can be calculated using its formula:
\(\frac{\vec{F}_1}{A_1} =\frac{\vec{F}_2}{A_2} \) or \(\frac{A_1}{A_2} =\frac{H_2}{H_1} \)
\(\vec{F}_1\) It is \(\vec{F}_2\) → applied and received forces, respectively, measured in Newton \([N]\).
\(TO 1\) It is \(A_2\) → areas related to the application of forces, measured in \([m^2]\).
\(H_1\) It is \(H_2\) → heights related to areas, measured in meters \([m]\).
Stevin's theorem measurement units
Several units of measurement are employed in Stevin's theorem. Next, we will see a table with the units of measurement according to the International System of Units (S.I.), another common way in which they appear and how to convert one into the other.
Stevin's theorem measurement units | |||
physical quantities |
Units of measurement according to the S.I. |
Units of measure in another format |
Conversion of measurement units |
Height |
m |
cm |
1 cm = 0.01 m |
Density or Especific mass |
\(kg/m^3\) |
\(g/mL\) |
Modification made by converting the units of measure of other physical quantities. |
gravity acceleration |
\(\frac{m}{s^2}\) |
\(\frac{km}{h^2}\) |
Modification made by converting the units of measure of other physical quantities. |
Pressure |
Shovel |
Atmosphere (atm) |
\(1\ atm=1.01\cdot10^5 \ Pa\) |
See too: Weight force — the attractive force existing between two bodies
Solved exercises on Stevin's theorem
question 1
(Unesp) The maximum pressure difference that a human lung can generate per inspiration is around \(0,1\cdot10^5\ Pa\) or \(0.1\atm\). Thus, even with the aid of a snorkel (vent), a diver cannot exceed a depth maximum, as the pressure on the lungs increases as he dives deeper, preventing them from inflate.
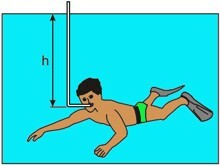
Considering the density of water \(10^3\ kg/m\) and the acceleration of gravity \(10\ m/s^2\), the estimated maximum depth, represented by h, that a person can dive breathing with the help of a snorkel is equal to
A) 1.1 ‧ 102 m
B) 1.0 ‧ 102 m
C) 1.1 ‧ 101 m
D) 1.0 ‧ 101 m
E) 1.0 ‧ 100 m
Resolution:
Alternative E
The pressure difference (Δp) can be given by Stevin's law:
\(∆p=d\cdot g\cdot ∆h\)
\(0,1\cdot10^5=10^3\cdot10\cdot∆h\)
\(0,1\cdot10^5=10^4\cdot∆h\)
\(∆h=\frac{0,1\cdot10^5}{10^4} \)
\(∆h=0.1\cdot10^{5-4}\)
\(∆h=0.1\cdot10^1\)
\(∆h=1\cdot10^0\ m\)
question 2
(Aman) A tank containing \(5.0\ x\ 10^3\) liters of water is 2.0 meters long and 1.0 meters wide. Being \(g=10\ m/s^2\), The hydrostatic pressure exerted by the water at the bottom of the tank is:
A) \(2.5\cdot10^4\ Nm^{-2}\)
B) \(2.5\cdot10^1\ Nm^{-2}\)
W) \(5.0\cdot10^3\ Nm^{-2}\)
D) \(5.0\cdot10^4\ Nm^{-2}\)
AND)\(2.5\cdot10^6\ Nm^{-2}\)
Resolution:
Alternative A
It is necessary to change the unit of measure for volume from liters to \(m^3\):
\(V=5\cdot10^3\ L=5\ m^3\)
The height will be given by:
\(5=1\cdot2\cdot h\)
\(5=2\cdot h\)
\(\frac{5}2=h\)
\(2.5=h\)
We will calculate the hydrostatic pressure exerted by the water at the bottom of the tank using Stevin's theorem:
\(p=d\cdot g\cdot h\)
Taking the density of water as \(1000\ kg/m^3 \) and gravity as \(10\ m/s^2\), we find:
\(p=1000\cdot10\cdot2.5\)
\(p=2.5\cdot10^4\ Pa=2.5\cdot10^4\ Nm^{-2}\)
Grades
|1| NUSSENZVEIG, Herch Moyses. Basic physics course: Fluids, Oscillations and Waves, Heat (vol. 2). 5 ed. São Paulo: Editora Blucher, 2015.
By Pamella Raphaella Melo
Physics Teacher
How about learning a little more about hydrostatics? This important branch of Physics is concerned with studying the properties of fluids in static equilibrium.
Do you know what specific mass is? Understand the difference between specific mass and density. Check out the formula used to calculate it. Learn more with exercises.
Principle of operation of machines.
Do you know what the Archimedes principle is? Access the text and discover the history of this principle. Learn the thrust formula and train with solved exercises.
Do you know Pascal's principle? According to this law, any pressure variation exerted on a fluid in equilibrium must be communicated equally by all parts of that fluid. Thanks to this property, it is possible to build hydraulic pistons, present in the most diverse types of mechanisms.
Click here to learn about the relationships between densities and pressures exerted by liquids contained in communicating vessels.


