THE 1st degree equation is an equation that has an unknown of degree 1. Equations are mathematical sentences that have unknowns, which are letters that represent unknown values, and equality. The mathematical sentence of the 1st degree equation is Thex + B = 0, where The and B are real numbers, and The is different from 0. The purpose of writing a 1st degree equation is to find the value of the unknown that satisfies the equation. This value is known as the solution or root of the equation.
Read too: Exponential equation — the equation that has at least one unknown in one of its exponents
Topics in this article
- 1 - Summary of 1st degree equation
- 2 - What is a 1st degree equation?
-
3 - How to calculate the first degree equation?
- → 1st degree equation with an unknown
- ? 1st degree equation with two unknowns
- 4 - Equation of the 1st degree in Enem
- 5 - Solved exercises on 1st degree equation
Summary of 1st degree equation
The 1st degree equation is a mathematical sentence that has 1 degree unknowns.
The 1st degree equation with one unknown has a unique solution.
The mathematical sentence that describes the 1st degree equation with one unknown is Thex + B = 0.
To solve a 1st degree equation with an unknown, we perform operations on both sides of the equality, in order to isolate the unknown and find its value.
The 1st degree equation with two unknowns has infinite solutions.
The mathematical sentence that describes the 1st degree equation with two unknowns is Thex + By + c = 0
The 1st degree equation is a recurring term in Enem, which usually comes with questions that require interpretation of the text and the assembly of the equation before solving it.
What is 1st Degree Equation?
Equation is a mathematical sentence that has an equality and one or more unknowns.. The unknowns are unknown values, and we use letters, such as x, y, z, to represent them.
What determines the degree of an equation is the exponent of the unknown. Thus, when the exponent of the unknown has degree 1, we have an equation of the 1st degree. See examples below:
2x + 5 = 9 (1st degree equation with one unknown, x)
y – 3 = 0 (1st degree equation with one unknown, y)
5x + 3y – 3 = 0 (1st degree equation with two unknowns, x and y)
Do not stop now... There's more after the ad ;)
How to calculate the first degree equation?
We represent a given situation as an equation when we aim to find the values that the unknown can take that makes the equation hold true, that is, find the solutions or the solution of the equation. Let's see below how to find the solution of a 1st degree equation with one unknown and the solutions of a 1st degree equation with two unknowns.
→ 1st degree equation with one unknown
THE 1st degree equation with one unknown is the equation of the type:
\(ax+b=0\ \)
In that sentence, The and B are real numbers. We use the equality symbol as a reference. Before it we have the 1st member of the equation and after the equal sign we have the 2nd member of the equation.
To find the solution to this equation, we seek to isolate the variable x. let's subtract B on both sides of the equation:
\(ax+b-b=0-b\ \)
\(ax=-\ b\)
Now we will divide by The on both sides:
\(\frac{ax}{a}=\frac{-b}{a}\)
\(x=\frac{-b}{a}\)
Important:This process of performing an action on both sides of the equation is often described as "passing to the other side" or "passing to the other side by doing the reverse operation".
Example 1:
Find the solution to the equation:
2x - 6 = 0
Resolution:
To isolate the variable x, let's add 6 to both sides of the equation:
\(2x-6+6\ =0+6\)
\(2x=6\)
Now, we will divide by 2 from both sides:
\(\frac{2x}{2}=\frac{6}{2}\)
\(x=3\ \)
We find as a solution to the equation x = 3. This means that if we substitute 3 in place of x, the equation will be true:
\(2\cdot3-6=0\)
\(6-6=0\ \)
\(0=0\)
Example 2:
We can solve the equation more directly using the practical method:
\(5x+1=-\ 9\)
First, let's define what is the first member of the equation and what is the second member of the equation:
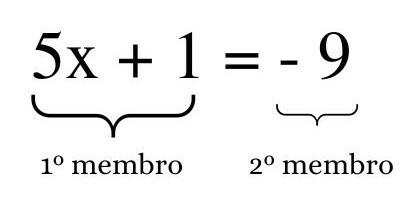
To find the solution of the equation, we will isolate the unknown on the first member of the equation. For this, what is not unknown will be passed to the second member doing the inverse operation, starting with + 1. As it is adding, it will pass to the second member by subtracting:
\(5x+1=-\ 9\ \)
\(5x=-\ 9-1\ \)
\(5x=-\ 10\)
We want the value of x, but we find the value of 5x. Since 5 is multiplying x, it will pass to the right hand side by doing the inverse operation of multiplication, that is, dividing.
\(5x=-\ 10\)
\(x=\frac{-10}{5}\)
\(x=-\ 2\)
The solution to this equation is x = - 2.
Example 3:
Solve the equation:
\(5x+4=2x-6\)
To solve this equation, we will initially put the terms that have an unknown on the first member, and the terms that do not have an unknown on the second member. To do this, let's identify them:
\({\color{red}5}{\color{red}x}+ 4 = {\color{red}2}{\color{red}x}\ –\ 6\)
In red are the terms that have an unknown, 5x and 2x, and in black, the terms that have no unknown. Since + 4 has no unknown, let's pass it to the second member by subtracting.
\(\color{red}{5x}=\color{red}{2x}-6-4\)
Note that 2x has an unknown, but is in the second member. We will pass it to the first member, subtracting 5x:
\({\color{red}{5x}-\color{red}{2x}=-6-4}\)
\(3x = - 10\)
Now, passing the 3 dividing, we have that:
\(x=-\frac{10}{3}\)
Important: The solution to an equation can be a fraction, as in the example above.
◆ Video lesson on 1st degree equation with an unknown
➝ 1st degree equation with two unknowns
When there is a 1st degree equation that has two unknowns, there is not a single solution, but rather infinite solutions. A 1st degree equation with two unknowns is an equation of the type:
\(ax+by+c=0\)
To find some of the infinite solutions of the equation, we assign a value to one of its variables and find the value of the other variable.
Example:
Find 3 possible solutions to the equation:
\(2x+y+3=0\)
Resolution:
To find 3 solutions, we will choose some values for the variable x, starting with x = 1:
\(2\cdot1+y+3=0\)
\(2+y+3=0\ \)
\(y+5=0\)
Isolating y in the first member, we have that:
\(y=0-5\)
\(y=-\ 5\)
So a possible solution to the equation is x = 1 and y = - 5.
To find one more solution of the equation, let's assign a new value to any of the variables. We will do y = 1.
\(2x+1+3=0\ \)
\(2x+4=0\ \)
Isolating x:
\(2x=-\ 4\ \)
\(x=\frac{-4}{2}\)
\(x=-\ 2\)
The second solution of this equation is x = - 2 and y = 1.
Finally, to find a third solution, we will choose a new value for one of your variables. We'll do x = 0.
\(2\cdot0+y+3=0\)
\(0+y+3=0\)
\(y+3=0\ \)
\(y=0-3\)
\(y=-\ 3\ \)
The third solution is x = 0 and y = -3.
We can represent these three solutions as ordered pairs, of the form (x, y). The solutions found for the equation were:
\(\left (1,-5\right);\ \left(-2,\ 1\right);\left (0,-3\right)\)
Important: Since this equation has two unknowns, we have infinite solutions. The values for the variables were chosen at random, so we could assign other completely different values to the variables and find three other solutions to the equation.
Know more: 2nd degree equation — how to calculate?
1st Degree Equation in Enem
Questions involving 1st degree equations in Enem require the candidate to be able to transform problem situations into equation, using utterance data. For clarity, see Mathematics area 5 competency.
Area 5 Competency: Model and solve problems involving socioeconomic or technical-scientific variables, using algebraic representations.
Note then that in Enem it is expected that the candidate can model problem situations of our daily life and solve them using an equation. Within this competence, there are two specific skills involving equations that Enem seeks to assess: skill 19 and skill 21.
H19: Identify algebraic representations that express the relationship between quantities.
H21: Solve a problem situation whose modeling involves algebraic knowledge.
So, if you are studying for the Enem, in addition to mastering the resolution of 1st degree equations, it is important to train in the interpretation of problems involving equations, because developing the ability to model problem situations by writing them as an equation, for Enem, is as important as being able to solve the equation.
Solved exercises on 1st degree equation
question 1
(Enem 2012) The supply and demand curves of a product represent, respectively, the quantities that sellers and consumers are willing to sell depending on the price of the product. In some cases, these curves can be represented by straight lines. Suppose that the quantities of supply and demand for a product are, respectively, represented by the equations:
QO = –20 + 4P
QD = 46 - 2P
in which QO is quantity of supply, QD is the quantity demanded and P is the price of the product.
From these supply and demand equations, economists find the market equilibrium price, that is, when QO and QD equal. For the situation described, what is the value of the equilibrium price?
a) 5
B) 11
C) 13
D) 23
E) 33
Resolution:
Alternative B
To find the equilibrium price, we simply equate the two equations:
\(Q_O=Q_D\)
\(–20+4P=46 –2P\)
\(4P+2P=46+20\)
\(6P=66\)
\(P=\frac{66}{6}\)
\(P=11\)
question 2
(Enem 2010) The triple jump is an athletics modality in which the athlete jumps on one foot, one step and one jump, in that order. The jump with take-off on one foot will be done so that the athlete lands first on the same foot that gave the take-off; in the stride he will land with the other foot, from which the jump is performed.
Available at: www.cbat.org.br (adapted).
An athlete of the triple jump modality, after studying his movements, realized that, from the second to the first jump, the range decreased by 1.2 m, and from the third to the second jump, the range decreased by 1.5 m. Wanting to reach the goal of 17.4 m in this event and considering your studies, the distance reached in the first jump would have to be between
A) 4.0 m and 5.0 m.
B) 5.0 m and 6.0 m.
C) 6.0 m and 7.0 m.
D) 7.0 m and 8.0 m.
E) 8.0 m and 9.0 m.
Resolution:
Alternative D
In the first jump, he reaches a distance of x meters.
In the second jump, the distance decreases by 1.2 m from the first jump, so he reaches a distance of x – 1.2 meters.
On the third hop, the distance decreases by 1.5 m from the second hop, so the distance covered on the third hop is x – 1.2 – 1.5 meters, which is the same as x – 2.7 meters.
We know that the sum of these distances must equal 17.4 meters, so:
\(x+x-1,2+x-2,7=17,4\)
\(3x-3.9=17.4\)
\(3x=17.4+3.9\)
\(3x=21.3\)
\(x=\frac{21,3}{3}\)
\(x=7.1\)
Thus, the distance reached in the first jump is between 7.0 and 8.0 meters.
By Raul Rodrigues de Oliveira
Maths teacher



