In mathematics, the fundamental difference between arrangement and combination is the order of objects. In the arrangement, the order of the objects is very important, that is, the objects must obey a stipulated order. In contrast, in the case of a combination, the order is of no importance.
| Arrangement | Combination | |
|---|---|---|
| Order | Is important. | It's not important. |
| Meaning | Arrangement refers to the different ways of arranging a set of objects in a sequential order. | Combination refers to the various ways of choosing items from a large pool of objects, so that their order does not matter. |
| denotes | Arrangement. | Selection. |
| What is it | Ordered elements. | Unordered sets. |
| sample question | A telephone number consists of 9 digits, from 0 to 9. So how many different phone numbers can we have? |
Among a group of 10 students, the teacher must choose 3 to make a presentation. Determine how many different ways the teacher can choose these students. |
Definition of Arrangement
In combinatorial analysis, arrangement are the different ways of arranging the objects of a set, in a specific order. This implies every arrangement or rearrangement that is possible.
For example, all possible array created with letters x, y, z would be:
- Using all three at a time: xyz, xzy, yxz, yzx, zxy, zyx;
- Using two at a time are xy, xz, yx, yz, zx, zy.
Example of arrangement in practice
Let's say your locker password is 5432. If you enter 4325 in it, it won't open because it's a different order.
Possible arrangements for 2, 3, 4, 5 are: 5432, 5423, 5324, 5342, 5234, 5243, 4532, 4523, 4325, 4352, 4253, 4235, 3542, 3524, 3425, 3452, 3254, 3 245, 2543, 2534, 2435, 2453, 2354, 2345.
We can say that your locker password is a specific arrangement of 2, 3, 4, and 5. If your locker worked by combination, you could insert any of the above arrangements and it would open!
Formula for calculating simple arrays
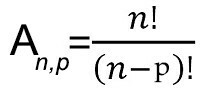
n = Total number of elements in the set
P = Number of elements per array
Definition of Combination
Combination is defined as the different ways of selecting a group, having some or all of the items in a set, without the order mattering.
As an example, these would be the possible combinations with the letters x, y, z:
- When all letters are used, the only combination is xyz.
- When two out of three letters are used, possible combinations are xy, xz, yz.
Formula to calculate combination

Example of the difference between arrangement and combination
Suppose there is a situation where you have to find the total number of possible samples of two out of three objects A, B, C. First you need to understand whether the question is related to arrangement or combination, and the only way to find out is to check whether order matters or not.
If the order is significant, then the question is related to the arrangement, and the possible samples will be AB, BA, BC, CB, CA, CA. In this case, AB is different from BA, BC is different from CB, and AC is different from CA.
If the order is irrelevant, the question is related to the combination, then the possible samples will be AB, BC and CA.
Also read about the difference between Digit, number and numeral.