bisector is the inner ray of an angle drawn from its vertex, dividing it in two angles congruent. The angle bisectors of a triangle meet at a point known as the incenter, which is the center of the circle inscribed in that polygon.
From the bisector, two important theorems were elaborated: the internal angle and the external angle, developed in triangles that use proportion to relate the sides of that polygon. In the Cartesian plane, it is possible to trace the bisector in odd and even quadrants.
Read too: Notable points of a triangle
bisector summary
A bisector is a ray that divides an angle into two congruent angles.
We can plot the bisectors of interior angles of triangles.
The interior angle theorem was developed from the bisector of an angle of the triangle.
There are two bisectors in the Cartesian plane, even quadrants and odd quadrants.
What is bisector?
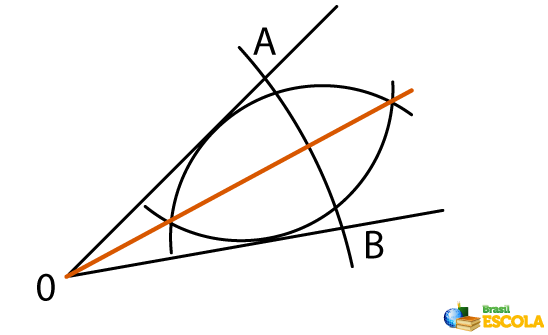
Given an angle AOB, we call the ray OC bisector, which starts at the point O and divides the angle AOB into two congruent angles.
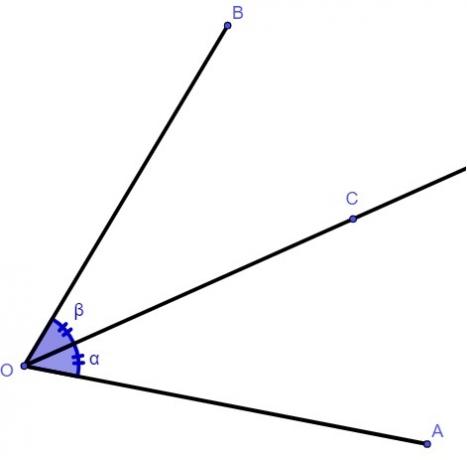
In the image, ray OC bisects angle AOB.
Do not stop now... There's more after the ad ;)
How to find the bisector?
To find the bisector, a ruler and a compass are used as instruments and the following steps are followed:
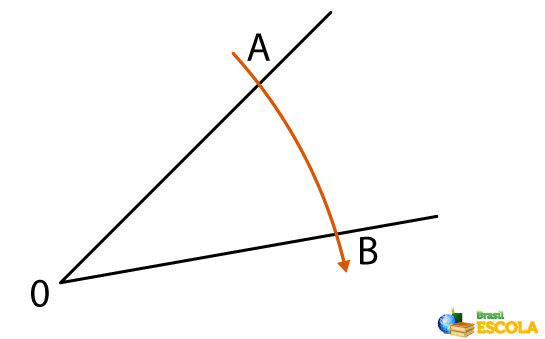
1st step: The dry point of the compass is placed under the vertex O and an arc is made over the rays OA and OB.
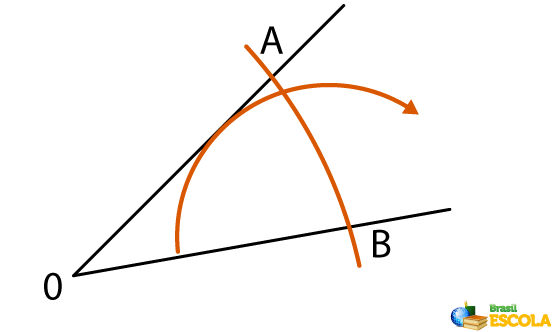
2nd step: The dry point of the compass is placed at the point of intersection of the arc with the ray OA and an arc is made with the compass facing the inner part of the angle.
3rd step: At the point of intersection of the arc with the ray OB, place the dry point of the compass and repeat the previous process.
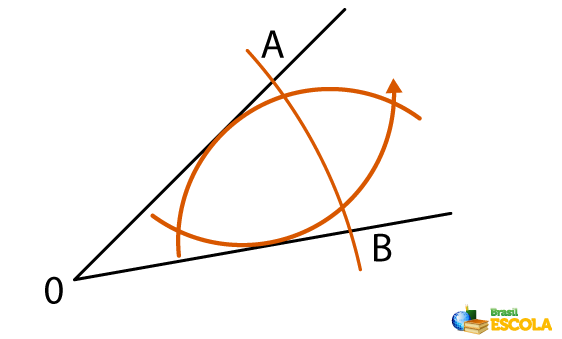
4th step: Finally, by drawing a ray from the vertex of the angle that passes through the points of intersection between the arcs, the angle bisector is found.
Read too: Barycenter — one of the notable points of a triangle
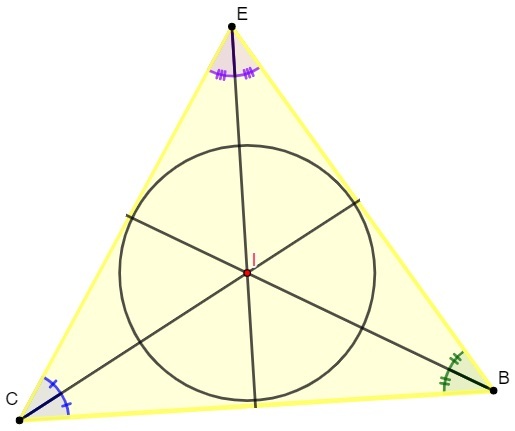
Bisector of a triangle
When bisectors of the interior angles of a triangle are traced, we can find its remarkable point, known as incenter, which is the meeting pointThe of bisectors and also the center of circumference inscribed in the polygon.
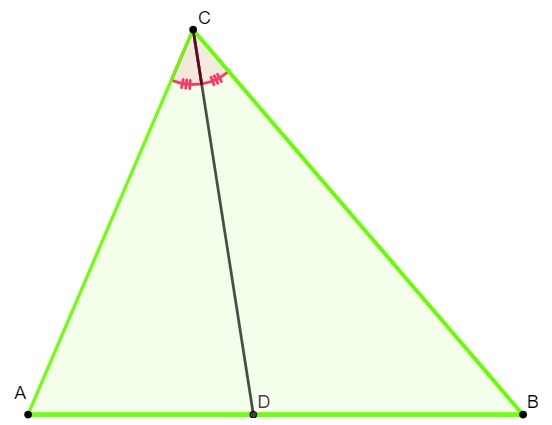
Internal Bisector Theorem
segments are formed proportional adjacent sides of a triangle when we bisector one of its interior angles.
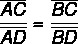
Example:
Given the following triangle, find the length of side AC.

Resolution:
Applying the internal bisector theorem, we calculate:

Video lesson on the internal bisector theorem
External Bisector Theorem
When the bisector of one of the exterior angles of a triangle is drawn, the prolongation of the side opposite the exterior angle forms proportional segments to adjacent sides.

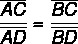
Example:
Find the value of x.
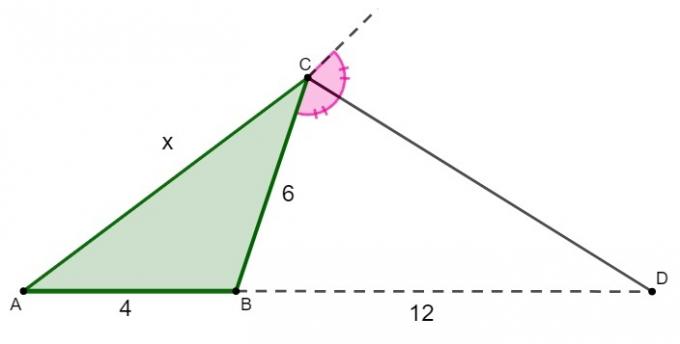
Applying the outer bisector theorem, we have:
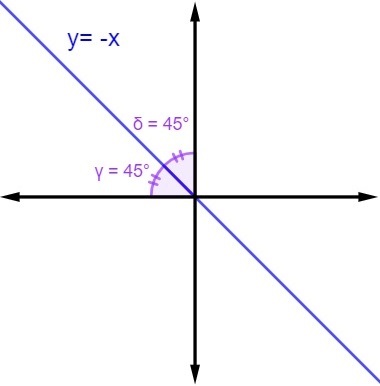
Bisector of quadrants of the Cartesian plane
It is possible to plot the bisector in the Cartesian plane. There are two possibilities: the bisector that passes through the even quadrants and the one that passes through the odd quadrants.
THE bisector of quadrants odd numbers pass through the 1st and 3rd quadrants. When the bisector cuts the odd quadrants, The your equation is y = x. Therefore, the points belonging to the bisector of the even quadrants have the same abscissa and ordinate.
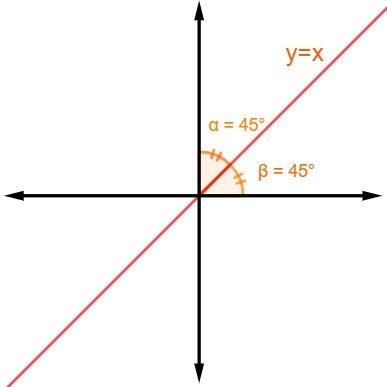
The second case concerns when the bisector passes through the even quadrants, that is, by the 2nd and 4th quadrants. When this occurs, the equation of the line will be y = – x. Therefore, the points have abscissa and ordinate as symmetric numbers.
Read too: Fundamental similarity theorem — the relationship between a parallel line and the side of a triangle
Solved exercises on bisector
question 1
In the following image, knowing that OC is the bisector of angle AOB, we can say that the measure of angle AOB is equal to

A) 15th
B) 30°
C) 35°
D) 60°
E) 70º
Resolution:
Alternative E
Since OC is a bisector, we have the following:
3x – 10 = 2x + 5
3x – 2x = 10 + 5
x = 15°
It is known that x = 15 and that the value of half the angle AOB is equal to 2x + 5. Substituting x by 15, we get:
2 · 15 + 5
30 + 5
35°
Half of the angle AOB is 35°. Therefore, the angle AOB is equal to twice 35°, that is,
AOC = 35 · 2 = 70°.
question 2
In a triangle, its three internal bisectors were drawn. After tracing them, it was possible to notice that they meet at a point. The point where the angle bisectors of a triangle meet is known as
A) centroid.
B) incenter.
C) circumcenter.
D) orthocenter.
Resolution:
Alternative B
When the internal bisectors of a triangle are drawn, their meeting point is known as the incenter.
By Raul Rodrigues de Oliveira
Maths teacher
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Raul Rodrigues de. "Bisetrix"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/bissetriz.htm. Accessed January 20, 2022.

