Root function is the function that has at least one variable inside a radical. It is also called an irrational function, the most common of which is square root, however there are others, such as the cube root function, among other possible indices.
To find the domain of a root function, it is important to analyze the index. When the index is even, the radicand must be positive by condition of existence of the root. The range of the root function is set of the real numbers. It is also possible to make graphical representation of a function source.
Know more:Domain, co-domain, and image—what does each represent?
Root function summary
THE occupation root is the one that has a variable inside the radical.
-
To find the domain of the root function, it is necessary to analyze the index of the radical.
If the root index is even, in the radicand there will only be positive real values.
If the root index is odd, the domain is the real numbers.
The square root function is the most common among the root functions.
The square root function has an ever-increasing and positive graph.
Do not stop now... There's more after the ad ;)
What is the root function?
We classify any function that has a variable inside the radical as root function. Analogously, we can consider as a root function the one that has a variable raised to an exponent equal to a fraction own, which are fractions that have the numerator smaller than the denominator, because whenever necessary we can transform a radical into a potency with fractional exponent.
Examples of root function:
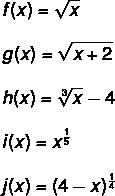
How to calculate the root function
Knowing the law of formation of a root function, one must calculate the numerical value of the function. As with all the functions we studied, we calculate the numerical value of the function by replacing the variable with the desired value.
Example of how to calculate the root function:
Given the function f(x) = 1 + √x, find the value of:
a) f (4)
Substituting x = 4, we have:
f (4) = 1 + √4
f(4) = 1 + 2
f(4) = 5
These functions are known as irrational. by the fact that most of your images are irrational numbers. For example, if we calculate f(2), f(3) for this same function:
b) f (2) = 1 + √2
c) f (3) = 1 + √3
We leave it represented in this way, as a addition between 1 and the irrational number. However, when necessary, we can use an approximation for these non-exact roots.
See too: Inverse function — the type of function that does the exact inverse of the function f(x)
Domain and range of a root function
When we study a root function, it is essential to analyze case by case, so that it is possible to define well The your domain. The domain directly depends on the root index and what is in its radicand. The range of a root function is always the set of real numbers.
Here are some examples:
Example 1:
Starting with the most common and simplest root function, the following function:
f(x) = √x
Analyzing the context, it is noted that, as it is a square function and the range is the set of real numbers, there is no negative root in the set when the index is even. Therefore, the domain of the function is the set of positive real numbers, that is:
D = R+
Example 2:

Since there is a square root, for this function to exist in the set of real numbers, or rooting must be greater than or equal to zero. So, we calculate:
x – 4 ≥ 0
x ≥ 4
So the domain of the function is:
D = {x ∈ R | x ≥ 4}
Example 3:
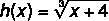
In this function there is no restriction, because the index of the root is odd, so the radicand can be negative. Thus, the domain of this function will be the real numbers:
D = R
Also access: Rooting — the numerical operation inverse to power
Graph of a root function
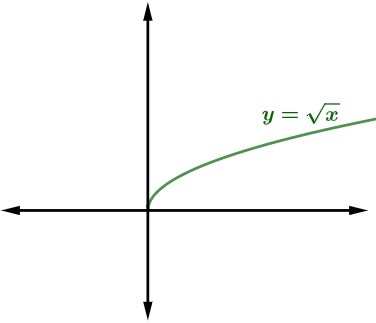
In the square root of x function, the graph is always positive. In other words, the range of the function is always a positive real number, the values x can take on are always positive, and the graph is always increasing.
Example of square root function:
Let's look at the graph representation of the square root function of x.
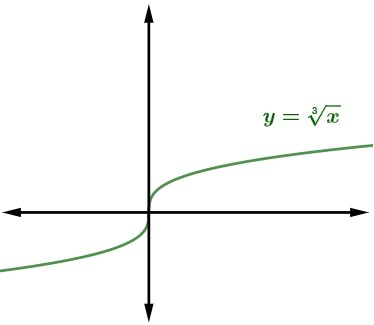
Example of cube root function:
Now, we will graph a function with an odd index. It is possible to represent other root functions, such as cubic functions. Next, let's look at the representation of the cube root function of x. Note that, in this case, as the root has an odd index, x can admit negative values, and the image can also be negative.
Read too:How to build the graph of a function?
Root function solved exercises
question 1
Given the following root function, with domain in the set of positive real numbers and range in the set of real numbers, what must be the value of x so that f(x) = 13?
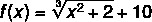
a) 3
B) 4
C) 5
D) 6
E) 7
Resolution:
Alternative C
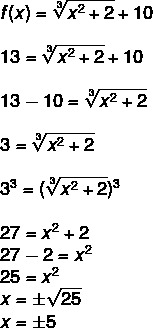
Since the domain of the function is the set of positive real numbers, the value that makes f(x) equal to 13 is x = 5.
question 2
About the function f(x), judge the following statements.
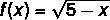
I → The domain of this function is the set of real numbers greater than 5.
II → In this function, f(1) = 2.
III → In this function, f( – 4) = 3.
Mark the correct alternative:
A) Only statement I is false.
B) Only statement II is false.
C) Only statement III is false.
D) All statements are true.
Resolution:
Alternative A
I → False
We know that 5 – x > 0, so we have:
– x > – 5 ( – 1)
x < 5
The domain is therefore real numbers less than 5.
II → True
Calculating f(1), we have:

III → True

By Raul Rodrigues de Oliveira
Maths teacher

