THE rectangle is one of flat figures more present in our daily lives. We can observe boxes, walls, tables and several other objects that have rectangular faces. A rectangle is a four-sided polygon and gets its name because it has all right angles, that is, measuring 90°. To calculate the area of a rectangle, we multiply its base by its height. The perimeter is equal to the sum of all its sides.
This shape is composed of 4 vertices and 4 sides. In a rectangle, we can draw two diagonals, and the length of these diagonals is calculated using the Pythagorean theorem. There are also the right trapezoid and the right triangle, which are so named because they have right angles.
Read too: Sum of the interior angles of a polygon — what mathematical expression can be used?
Summary about rectangle
The rectangle is a polygon which has 4 right angles.
To calculate the area of a rectangle, we multiply its base and height.
The perimeter of a rectangle is equal to the sum of all its sides.
In a rectangle, we can draw two diagonals.
The diagonal of the rectangle divides the rectangle into two triangles, so the Pythagorean theorem can be applied.
If a trapezoid has two of its right angles, it is called a right-angled trapezoid.
If we divide the rectangle in half by one of its diagonals, we find a right triangle.
Elements of a rectangle
Geometric shapes surround us in our daily lives, and the rectangle is a very common shape. the rectangle has four right angles, that is, its interior angles measure 90°.

There are other important elements in a rectangle besides its 4 right angles. Are they:
their vertices;
its sides;
its diagonals.
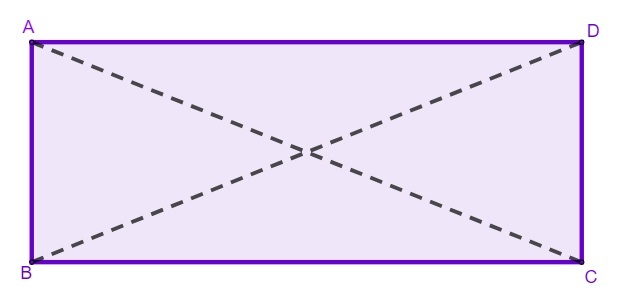
As can be seen in the figure above,
A, B, C and D are the vertices of the rectangle;
AB, AD, BC and CD are the sides of the rectangle;
AC and BC are the diagonals of the rectangle.
rectangle properties
the rectangle it hasopposite sides parallel, which makes it classified as a parallelogram. Because it is a parallelogram, it has important properties. Are they:
congruent opposite sides;
internal angles measuring 90°;
exterior angles that also measure 90°;
congruent diagonals;
diagonals that meet at the midpoint.
Know more: Square — figure that belongs to the set of quadrilaterals
rectangle formulas
There are important formulas involving rectangles, used to calculate the measurement of their area, perimeter and diagonals.
rectangle area
To calculate the measurement of the surface of a rectangle, that is, its area, we perform the multiplication from the base by the height:
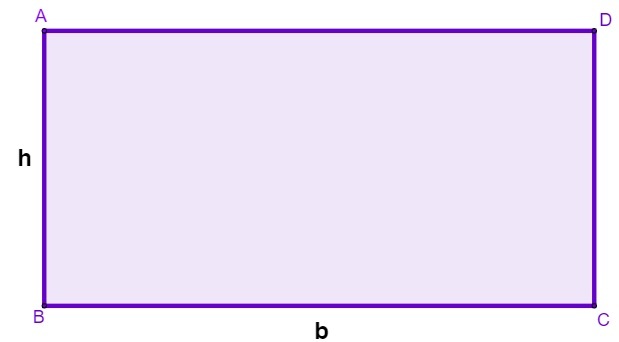
\(A\ =\ b\ \cdot h\ \)
b ➜ rectangle base
h ➜ rectangle height
Important: Note that in a rectangle the height coincides with the length of sides AB and DC.
→ Example of calculating the area of a rectangle
A plot of land has a rectangular shape with a base measuring 7.5 meters and a height of 5 meters. What is the area of this land?
Resolution:
To calculate the area, simply multiply between 7.5 and 5:
\(A\ =\ 7.5\ \cdot5\)
\(A=37.5m^2\)
Also know: Areas of plane figures — the formulas according to each geometric shape
perimeter of the rectangle
The calculation of perimeter of any plane figure is given by sum from your sides. In a rectangle, since opposite sides are congruent, we can calculate the perimeter using the formula:
\(P=2\left (b+h\right)\)
→ Example of calculating the perimeter of a rectangle
What is the perimeter of a rectangular piece of land that has sides measuring 7.5 meters and 5 meters?
Resolution:
We know that the perimeter is the sum of all sides, so we have:
\(P=2\ \left (7.5+5\right)\)
\(P\ =\ 2\ \cdot12,5\ \)
\(P\ =\ 25\ m\)
Rectangle Diagonal
When tracing the diagonal of a rectangle, we notice that it divides the rectangle into two triangles. From there, it is possible to applyThe Pythagorean theorem in the right triangle formed.

→ Example of calculating the diagonal of a rectangle
What is the diagonal of a rectangle whose base is 8 cm and height 6 cm?
Resolution:
Calculating the diagonal:
d² = 8² + 6²
d² = 64 + 36
d² = 100
d = \(\sqrt{100}\)
d = 10 cm
rectangle trapezoid

A trapezoid is a polygon that has four sides, two of which are parallel and the other two are not. A trapezoid is called a right-angled trapezoid when has two of its right angles.
right triangle
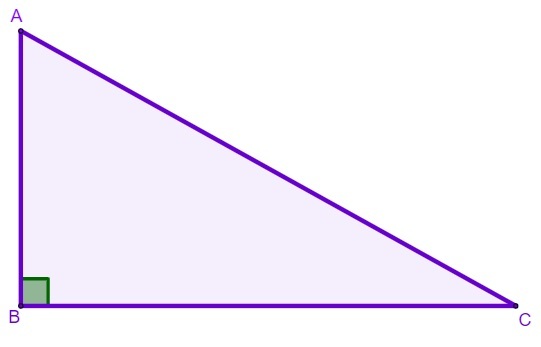
THE triangle rectangle is studied in depth in the Plane Geometry, making possible the development of important theorems, such as the Pythagorean theorem, in addition to the studies of Trigonometry. As we saw earlier, if we divide the rectangle in half by one of its diagonals, we will find a right triangle, because the triangle is considered a right triangle when it has an internal angle of 90°.
Video lesson on Plane Geometry
Exercises solved on the rectangle
question 1
In the farm of Seu João, an area in the shape of a rectangle was set aside for the cultivation of corn. Before planting, Seu João decided to surround this area with 4 loops of barbed wire, to make it difficult for animals and people to enter. Knowing that the cultivation area is 22 meters wide and 18 meters long, what is the minimum amount of wire needed to fence the region?
A) 80 meters
B) 160 meters
C) 240 meters
D) 320 meters
Resolution:
Alternative D
First, we will calculate the perimeter of this region:
\(P=2\cdot\left (22+18\right)\)
\(P\ =\ 2\cdot40\ \)
\(P\ =\ 80\ m\ \)
Knowing that the perimeter is 80 meters, we will multiply 80 by 4, since there will be 4 turns:
\(80\ \cdot4\ =\ 320\ m\ \)
question 2
What is the area of the following rectangle, given that its sides are measured in meters?

A) 45 m²
B) 180 m²
C) 240 m²
D) 252 m²
Resolution:
Alternative D
We know that opposite sides are equal. So, to find the value of x, we have:
\(3x\ -\ 1\ =\ 2x\ +\ 4\ \)
\(3x\ -\ 2x\ \ =\ 4\ +\ 1\ \)
\(x\ =\ 5\ \)
Now, we will find the value of y:
\(3y\ -\ 3\ =\ y\ +\ 6\ \)
\(3y\ -\ y\ =\ 6\ +\ 3\ \)
\(2y\ =\ 9\)
\(y=\frac{9}{2}\)
\(y\ =\ 4.5\ \)
To calculate the area, you need to find the length of the sides. Therefore, we will substitute the value found for x in the base equation and the value found for y in the height equation.
\(2x\ +\ 4\ =\ 2\ \cdot10\ +\ 4\ =\ 20\ +\ 4\ =\ 24\ \)
\(y\ +\ 6\ =\ 4.5\ +\ 6\ =\ 10.5\ \)
Calculating the area, we have:
\(A\ =\ b\ \cdot h\)
\(A\ =\ 24\ \cdot10,5\ \)
\(A=252\ m^2\)


