Triangle is a polygon with three angles, sides and vertices, which belong to the same plane. This polygon, always convex, is the junction of the three non-collinear line segments that, in pairs, form the three angles and delimit its internal region.
This figure is widely used with various applications. In engineering, as it is a rigid element, which does not deform, it grants stability to structures.
Among all, this is the only polygon that does not have a diagonal, in addition to presenting itself in several formats. They are classified according to the characteristics of the length of the sides and measures of their angles.
types of triangles
Triangles can be classified by sides and angles, with three main types for each.
Obtuangle, Rectangle and Acute Angle
In relation to the angles, the triangles are classified having as parameter the angle of 90º.
obtuse angle
An obtuse triangle has an obtuse angle, that is, greater than 90°. This makes the other two smaller than 90º.

Rectangle
A right triangle is one that, as its name suggests, has a right angle of 90 degrees.

acute
An acute triangle is one with three angles less than 90°.

In addition to the types of triangles in relation to angles, the length of the sides also classifies them into three categories.
Equilateral, isosceles and scalene
Regarding the sides, the criteria for classifying triangles are their lengths, being: all three are equal, only two are equal, or none are equal.
Equilateral
The equilateral triangle has three sides of the same measure, which leads to it having the three interior angles also equal, with 60º.

Isosceles
The isosceles triangle has two sides with the same length and, due to this, the two angles referring to the base are also equal.

Scalene
A scalene triangle has three sides with different measures and, consequently, three angles with different measures.

learn more about classification of triangles.
triangle area
The measurement of the area, the inner region, bounded by the three sides of a triangle, can be calculated in a few ways. Each offers its calculation advantages, depending on the information available.
A widely used mode is the one that depends on the measurement of the base and height.
Where,
THE is the area,
B is the measure of the base,
H is the height measurement.
Heron's formula for the area of a triangle
It is also possible to calculate the area of a triangle with Heron's formula, which uses the measures of the three sides and does not depend on height.
Where,
P is the semiperimeter, that is, half the perimeter, calculated as:
Where The, B and ç are the measurements of the sides.
See more about triangle area.
perimeter of the triangle
The perimeter is the sum of the measures of the sides of any polygon. Since the triangle has three sides:
where a, b and c are the lengths of the sides.
learn more about perimeter of the triangle.
Condition of existence of a triangle
For a triangle to exist, its sides must meet at the vertices. However, not every trio of segments satisfies this condition.
In order for a triangle to be formed, the measure of each side must be less than the sum of the other two.
Considering any triangle, with sides a, b and c, in order for this triangle to be constructed, it must be satisfied:
Height, bisector, median and bisector
These four geometric elements are extremely important in the study of triangles. They give characteristics and properties to triangles. Since they all refer to sides and angles, every triangle will have three of the following elements:
Height
The height is a line segment that connects a vertex to the opposite side, forming a 90º angle with the side it intersects, or its extension.

The height of a triangle can be inside or outside. Since there are three sides, there will be three heights, one relative to each side.
Mediatrix
A bisector is a line that cuts the midpoint of one side of the triangle, forming a 90º angle.
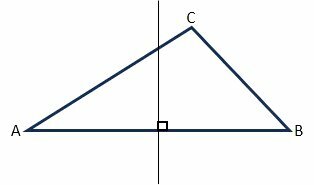
The bisector in relation to the side AB, intersects it at its midpoint, that is, in the middle, forming an angle of 90º with this side.
see more than bisector.
median
The median is a segment that connects a vertex to the midpoint of the opposite side.
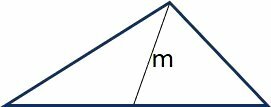
Although the median also divides the side opposite the angle into two equal parts, unlike the bisector, it does not make a 90º angle with the side.
bisector
A bisector is a ray that divides an angle in half.
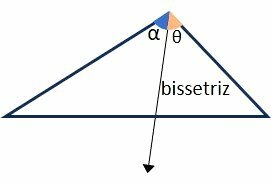
Since the bisector divides an angle into two equal ones, we have that .
Notable points of a triangle
In a triangle there are four notable points, formed by the intersections between the three altitudes, bisectors, bisectors, and medians. These points can be internal or external to the triangles and give it characteristics and properties.
orthocenter
The orthocenter is the point of intersection between the three heights.

The orthocenter can be internal, external or belong to the triangle. Internal if the triangle is acute, external if it is obtuse and belong to the triangle if it is a right triangle.

circumcenter
It is the meeting point of the three bisectors.
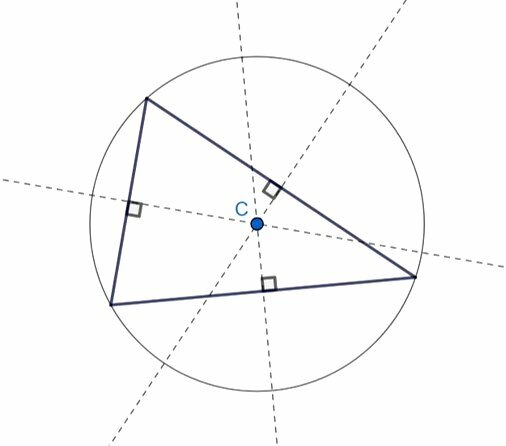
The circumcenter is the center of the circle circumscribed to the triangle.
incenter
It is the meeting point of bisectors.
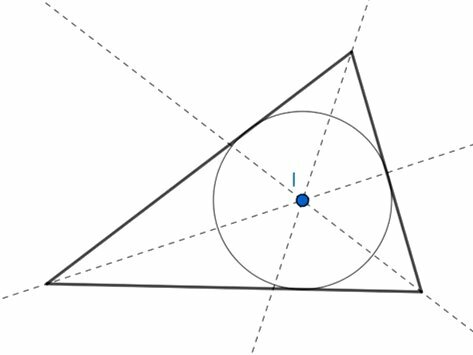
The incenter is the center of the circle inscribed in the triangle.
Barycenter
It is the point of intersection between the medians.
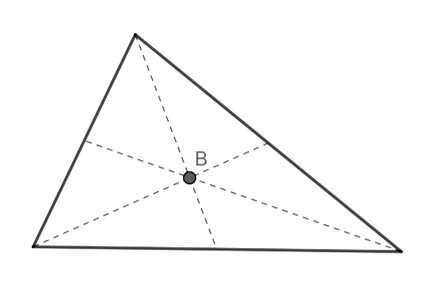
The centroid is the center of mass or, of gravity, of the triangle.
Interior and exterior angles of the triangle
In a triangle, the sum of the three interior angles is equal to 180°.
Where,are the interior angles of the triangle.
external angle
An exterior angle is formed between the extension of one side and the adjacent side. Every exterior angle is supplementary to the interior, that is, they add up to 180°.
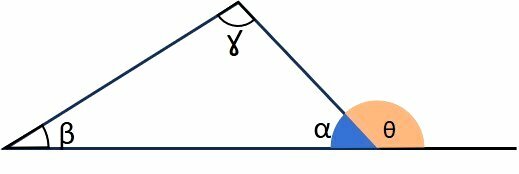
In the image, is an exterior angle, supplementary to the interior angle, that is,
.
exterior angle theorem
The exterior angle theorem says that the measure of an exterior angle is equal to the sum of the other two interior angles.
Regarding the angle highlighted in the figure, we have:
Inscribed and circumscribed triangle
a triangle registered a circle is interior to it and its vertices lie on the line of the circle.

The points of the vertices A, B and C also belong to the circle.
At the equilateral triangle inscribed in the circle, the measure of the side relates to the radius of the circle, as:
Where L is the length of the side and R is the radius.
a triangle circumscribed to a circle is exterior to it, and the circle is tangent to the sides of the triangle.
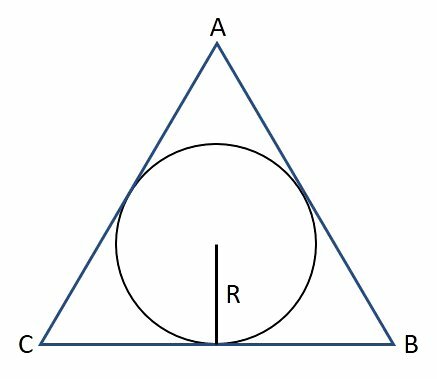
One equilateral triangle circumscribed to a circle is related to its radius, by:
Where L is the length of the side and R is the radius.
See too:
- right triangle
- Equilateral triangle
- Scalene Triangle
- Isosceles Triangle
- Similarity of Triangles
- Similarity of Triangles - Exercises
- Pythagorean theorem
- Classification of Triangles
- Isosceles Triangle
- Mediatrix
- bisector
- Exercises on Polygons
- Triangle Area
- Plane Geometry
- quadrilaterals