Euler's relation: vertices, faces and edges

Euler's relation is an equality that relates the number of vertices, edges and faces in convex polyhedra. It says that the number of faces plus the number of vertices is equal to the number of edges plus two.

The Euler relation is given by:

Where,
F is the number of faces,
V the number of vertices,
THE the number of edges.

We can use Euler's relation to determine or confirm unknown values ​​of V, F or A, whenever the polyhedron is convex.

Polyhedron	F	V	THE	F+V	A + 2
Cube	6	8	12	6 + 8 = 14	12 + 2 = 14
triangular pyramid	4	4	6	4 + 4 = 8	6 + 2 = 8
Pentagonal base prism	7	10	15	7 + 10 = 17	15 + 2 = 17
regular octahedron	8	6	12	8 + 6 = 14	12 + 2 = 14

Example
A convex polyhedron has 20 faces and 12 vertices. Determine the number of edges.

Using Euler's relation and isolating A:

Substituting the values ​​of F and V:

Faces, Vertices and Edges

Polyhedra are solid, three-dimensional geometric shapes without rounded sides. These sides are the faces (F) of the polyhedron.

The meeting of the faces, we call edges (A).

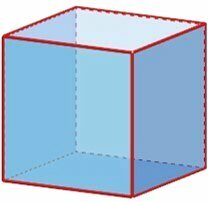
Vertices are the points where three or more edges meet.

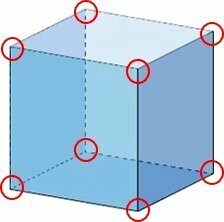
convex polyhedra

Convex polyhedra are geometric solids that do not present concavity, therefore, on none of their faces there are internal angles greater than 180º.

Convex polyhedron: all internal angles of the faces less than 180º.

Non-convex polyhedron: has at least one interior angle greater than 180°.

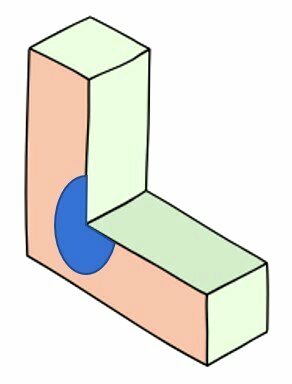
In this polyhedron, the internal angle marked in blue has more than 180º, so it is not a convex polyhedron.

See more about polyhedra.

Exercises on Euler's Relation

Exercise 1

Find the number of faces in a polyhedron with 9 edges and 6 vertices.

see answer

Correct answer: 5 faces.

Using Euler's relation:

F + V = A + 2
F = A + 2 - V
F = 9 + 2 - 6
F = 11 - 6
F = 5

Exercise 2

A dodecahedron is a Platonic solid with 12 faces. Knowing that it has 20 vertices, determine its number of edges.

see answer

Right answer:

Using Euler's relation:

F + V = A + 2
F + V - 2 = A
12 + 20 - 2 = A
32 - 2 = A
30 = A

Exercise 3

What is the name of the polyhedron with 4 vertices and 6 edges in relation to its number of faces, where the faces are triangles?

see answer

Answer: Tetrahedron.

We need to determine its number of faces.

F + V = A + 2
F = A + 2 - V
F = 6 + 2 - 4
F = 8 - 4
F = 4

A polyhedron that has 4 faces in the form of triangles is called a tetrahedron.

Who was Leonhard Paul Euler?

Leonhard Paul Euler (1707-1783) was one of the most proficient mathematicians and physicists in history, as well as contributing to astronomy studies. A German-speaking Swiss, he was professor of physics at the St Petersburg Academy of Sciences and later at the Berlin Academy. He published several studies on Mathematics.

Also learn:

• Geometric solids
• Spatial Geometry
• Geometric Shapes
• Prism - Geometric Figure
• Pyramid
• Paving stone
• Cube