The sum of the interior angles of a convex polygon can be determined knowing the number of sides (n), simply subtracting this value by two (n - 2) and multiplying by 180°.
A polygon is a closed surface formed by a polygonal line, that is, the sides are straight lines, and the meeting between two sides forms an angle. In case the polygon is convex, all interior angles are less than 180°.
Sum of the interior angles of a convex polygon
To add the interior angles of a convex polygon, either we know the values of all the angles and add them, or we can determine the sum by knowing the number of sides of this polygon.
Knowing the total sides of a polygon is, in many cases, easier information to obtain than the values of each angle.
Formula for the sum of interior angles of a polygon
To determine the sum of the interior angles of a convex polygon knowing only the number of sides, we use the formula:
Where,
yes is the sum, the total of degrees of all angles.
no is the number of sides.
Example
The sum of the interior angles of a quadrilateral is:
Since a quadrilateral has 4 sides, n is equal to 4.
Sum of the interior angles of a regular polygon
The sum of the interior angles of a regular polygon is calculated in the same way. A polygon is regular when all sides and angles are equal. The number of angles is always equal to the number of sides.
Interior angle of a regular polygon
As all angles have the same measure, it is enough to divide the sum of the interior angles by the number of angles, therefore, the number of sides.
Where,
Si is the sum, the total of degrees of all angles.
n is the number of sides.
Example
The measure of the interior angles of a regular pentagon is:
First we determine the sum of its interior angles using n = 5.
Now, just divide by the number of sides.
Name of polygons based on sides
Name some polygons depending on the number of sides.
| number of sides | Name |
|---|---|
| 3 | Triangle |
| 4 | quadrilateral |
| 5 | Pentagon |
| 6 | Hexagon |
| 7 | Heptagon |
| 8 | Octagon |
| 9 | enagon |
| 10 | Decagon |
| 11 | undecagon |
| 12 | Dodecagon |
| 20 | icosagon |
Deduction of the formula for the sum of the interior angles of a polygon
We start from the premise that every triangle has 180° as the sum of its interior angles.
From any vertex of a convex polygon, we can draw diagonals and form triangles.
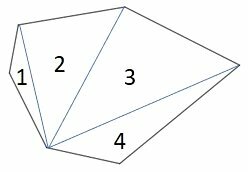
Since the sum of the interior angles of each triangle is equal to 180°, simply multiply the number of triangles formed by 180°.
We can see that the number of triangles formed is always equal to the number of sides minus 2.
For a triangle, n = 3.
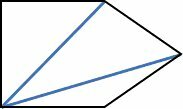
For a quadrilateral, n = 4.

There are 2 triangles:
For a pentagon, n = 5.
There are 3 triangles:
In this way, we can generalize and replace the term number of triangles by (n-2) and the formula looks like this:
learn more about polygons and angles.
Exercises
Exercise 1
Find the sum of the interior angles of a convex polygon with 17 sides.
Answer: 2 700º
Exercise 2
What is the name of a polygon whose interior angles sum to 1440°?
Answer: The polygon whose sum of the interior angles is 1440° is called a decagon, and has 10 sides.
Exercise 3
Find the value of the interior angles of a regular octagon.
Answer: In a regular octagon, each interior angle measures 135°.
First we must determine the sum of the interior angles of an octagon. Since it has eight sides, n = 8.
As the polygon is regular, all the interior angles have the same measure, and just divide the total by 8.
practice more polygon exercises.
See too:
- Area and Perimeter
- Polygon Area
- Hexagon
- quadrilaterals
- parallelogram